त्रिभुज का मध्यखंड. समलंब चतुर्भुज, समलम्ब चतुर्भुज की मध्य रेखा, त्रिभुज

त्रिभुज की मध्य रेखा. नमस्कार दोस्तों! आज सैद्धांतिक सामग्री है, वह त्रिभुज से जुड़ी है। परीक्षा में कार्यों का एक समूह होता है जो इसकी मध्य रेखा की संपत्ति का उपयोग करता है। और न केवल त्रिभुजों की समस्याओं में, बल्कि समलम्ब चतुर्भुजों की समस्याओं में भी। एक ऐसा था जिसमें मैंने केवल इन तथ्यों को याद रखने का सुझाव दिया था, अब और अधिक विस्तार से...

त्रिभुज की मध्य रेखा क्या है और इसके गुण क्या हैं?

परिभाषा।त्रिभुज की मध्य रेखा त्रिभुज की भुजाओं के मध्य बिंदुओं को जोड़ने वाला एक खंड है।

स्पष्ट है कि त्रिभुज में तीन मध्य रेखाएँ होती हैं। आइए उन्हें दिखाएं:

बिना किसी प्रमाण के, आपने शायद पहले ही देख लिया होगा कि बनने वाले सभी चार त्रिभुज बराबर हैं। यह सच है, लेकिन हम इस बारे में बाद में अधिक विस्तार से बात करेंगे।

प्रमेय. किसी त्रिभुज की दो भुजाओं के मध्य बिंदुओं को जोड़ने वाली मध्य रेखा तीसरी भुजा के समानांतर और उसके आधे के बराबर होती है।

सबूत:

1. आइए त्रिभुज BMN और BAC को देखें। शर्त के अनुसार, हमारे पास BM=MA, BN=NC है। हम लिख सकते हैं:

इसलिए, त्रिभुज दो आनुपातिक भुजाओं और उनके बीच के कोण (समानता का दूसरा चिह्न) में समान होते हैं। इससे क्या निष्कर्ष निकलता है? लेकिन तथ्य यह है कि:

रेखाओं की समानता के आधार पर MN||AC.

2. त्रिभुजों की समानता से भी यह निष्कर्ष निकलता है

यानी एमएन दो गुना छोटा है। सिद्ध किया हुआ!

आइए एक सामान्य समस्या का समाधान करें।

त्रिभुज ABC में, बिंदु M, N, K भुजाओं AB, BC, AC के मध्यबिंदु हैं। यदि MN=12, MK=10, KN=8 है तो त्रिभुज ABC का परिमाप ज्ञात कीजिए।

समाधान। बेशक, सबसे पहले आपको त्रिभुज एमएनके (और इसलिए त्रिभुज एबीसी के अस्तित्व) के अस्तित्व की जांच करनी चाहिए। दो छोटी भुजाओं का योग तीसरी भुजा से अधिक होना चाहिए, 10+8>12 लिखें। पूरी होगी, इसलिए त्रिकोण मौजूद है।

आइए एक स्केच बनाएं:

इस प्रकार, त्रिभुज ABC का परिमाप 24+20+16=60 है।

*अब तीनों मध्य रेखाओं के निर्माण से प्राप्त त्रिभुजों के बारे में अधिक जानकारी। उनकी समानता आसानी से सिद्ध हो जाती है। देखना:

वे तीन तरफ से बराबर हैं। बेशक, अन्य संकेत भी यहां लागू होते हैं। हमें वह मिल गया

परीक्षा में शामिल कार्यों में इस संपत्ति का उपयोग कैसे किया जाता है? मैं विशेष रूप से स्टीरियोमेट्री की समस्याओं पर ध्यान केंद्रित करना चाहूंगा। ऐसे प्रकार हैं जिनमें हम त्रिकोणीय प्रिज्म के बारे में बात कर रहे हैं।

उदाहरण के लिए, ऐसा कहा जाता है कि विमान आधार के किनारों के मध्य बिंदुओं से होकर गुजरता है और यह आधार के तीसरे किनारे के समानांतर होता है। प्रिज्म के सतह क्षेत्र, उसके आयतन और अन्य में परिवर्तन के बारे में प्रश्न उठाए जाते हैं।

तो यह यहाँ है. ऊपर प्रस्तुत जानकारी को जानने और समझने से, आप तुरंत यह निर्धारित कर लेंगे कि यह विमान निर्दिष्ट प्रिज्म के आधार से एक चौथाई भाग काट देता है और समस्या को मौखिक रूप से हल कर देगा। ऐसे कार्यों के साथ.

बस इतना ही! शुभकामनाएं!

लेख सामग्री डाउनलोड करें

साभार, अलेक्जेंडर क्रुतित्सिख।

चित्र 1 दो त्रिभुज दिखाता है। त्रिभुज ABC त्रिभुज A1B1C1 के समान है। और आसन्न भुजाएँ आनुपातिक हैं, अर्थात AB, A1B1 के समानुपाती है, जैसे AC, A1C1 के समानुपाती है। इन दोनों स्थितियों से त्रिभुजों की समानता निकलती है।

त्रिभुज की मध्य रेखा कैसे ज्ञात करें - रेखाओं की समानता का संकेत

चित्र 2 रेखाएँ a और b, छेदक c दिखाता है। इससे 8 कोने बनते हैं. कोण 1 और 5 संगत हैं, यदि रेखाएँ समानांतर हैं, तो संगत कोण बराबर हैं, और इसके विपरीत।

त्रिभुज की मध्य रेखा कैसे ज्ञात करें

चित्र 3 में, M, AB का मध्य है, और N, AC का मध्य है, BC आधार है। खंड एमएन को त्रिभुज की मध्य रेखा कहा जाता है। प्रमेय स्वयं कहता है: त्रिभुज की मध्य रेखा आधार के समानांतर और उसके आधे के बराबर होती है।

यह सिद्ध करने के लिए कि एमएन एक त्रिभुज की मध्य रेखा है, हमें त्रिभुजों की समानता के लिए दूसरे परीक्षण और रेखाओं की समानता के लिए परीक्षण की आवश्यकता है।

दूसरे मानदंड के अनुसार, त्रिभुज AMN, त्रिभुज ABC के समान है। समान त्रिभुजों में, संगत कोण बराबर होते हैं, कोण 1 कोण 2 के बराबर होता है, और ये कोण तब संगत होते हैं जब दो रेखाएँ एक तिर्यक रेखा के साथ प्रतिच्छेद करती हैं, इसलिए, रेखाएँ समानांतर होती हैं, MN BC के समानांतर होता है। कोण A उभयनिष्ठ है, AM/AB = AN/AC = ½

इन त्रिभुजों का समरूपता गुणांक ½ है, इसका तात्पर्य यह है कि ½ = MN/BC, MN = ½ BC


इसलिए हमने त्रिभुज की मध्य रेखा ढूंढी, और त्रिभुज की मध्य रेखा के बारे में प्रमेय को सिद्ध किया, यदि आप अभी भी नहीं समझ पाए हैं कि मध्य रेखा कैसे खोजें, तो नीचे दिया गया वीडियो देखें।

किसी त्रिभुज की मध्य रेखा उसकी दो भुजाओं के मध्य बिंदुओं को जोड़ने वाला एक खंड है। तदनुसार, प्रत्येक त्रिभुज में तीन मध्य रेखाएँ होती हैं। मध्य रेखा की गुणवत्ता, साथ ही त्रिभुज की भुजाओं की लंबाई और उसके कोणों को जानकर, आप मध्य रेखा की लंबाई निर्धारित कर सकते हैं।

आपको चाहिये होगा

• त्रिभुज की भुजाएँ, त्रिभुज के कोण

निर्देश

1. माना त्रिभुज ABC MN में भुजाओं AB (बिंदु M) और AC (बिंदु N) के मध्य बिंदुओं को जोड़ने वाली मध्य रेखा है। गुण के अनुसार, 2 भुजाओं के मध्य बिंदुओं को जोड़ने वाली त्रिभुज की मध्य रेखा तीसरी भुजा के समानांतर होती है और आधे के बराबर होती है यह। इसका मतलब यह है कि मध्य रेखा एमएन भुजा BC के समानांतर और BC/2 के बराबर होगी। नतीजतन, त्रिभुज की मध्य रेखा की लंबाई निर्धारित करने के लिए, इस विशेष तीसरी भुजा की लंबाई जानना पर्याप्त है।

2. आइए अब उन पक्षों को जानें, जिनके मध्य बिंदु मध्य रेखा एमएन, यानी एबी और एसी, साथ ही उनके बीच के कोण बीएसी से जुड़े हुए हैं। क्योंकि MN मध्य रेखा है, तो AM = AB/2, और AN = AC/2। फिर, कोसाइन प्रमेय के अनुसार, वस्तुनिष्ठ रूप से: MN^2 = (AM^2)+(AN^2)-2*AM *AN*cos (BAC) = (AB^2/4)+(AC^2/4)-AB*AC*cos(BAC)/2. इसलिए, MN = sqrt((AB^2/4)+(AC^2/4)-AB*AC*cos(BAC)/2)।

3. यदि भुजाएँ AB और AC ज्ञात हैं, तो कोण ABC या ACB जानकर मध्य रेखा MN ज्ञात की जा सकती है। मान लीजिए कि एबीसी कोना प्रसिद्ध है। चूँकि मध्य रेखा के गुण के अनुसार MN, BC के समानांतर है, तो कोण ABC और AMN संगत हैं, और, परिणामस्वरूप, ABC = AMN है। फिर, कोसाइन प्रमेय के अनुसार: AN^2 = AC^2/4 = (AM^2)+(MN^2)-2*AM*MN*cos(AMN)। नतीजतन, एमएन पक्ष द्विघात समीकरण (MN^2)-AB*MN*cos(ABC)-(AC^2/4) = 0 से पाया जा सकता है।

एक वर्ग त्रिभुज को अधिक सही ढंग से समकोण त्रिभुज कहा जाता है। त्रिकोणमिति के गणितीय अनुशासन में इस ज्यामितीय आकृति की भुजाओं और कोणों के बीच संबंधों पर विस्तार से चर्चा की गई है।

आपको चाहिये होगा

• - कागज़;
• - कलम;
• - ब्रैडिस टेबल;
• - कैलकुलेटर।

निर्देश

1. खोज करना ओरआयताकार त्रिकोणपाइथागोरस प्रमेय के समर्थन से। इस प्रमेय के अनुसार, कर्ण का वर्ग पैरों के वर्गों के योग के बराबर है: c2 = a2+b2, जहां c कर्ण है त्रिकोण, ए और बी इसके पैर हैं। इस समीकरण को लागू करने के लिए, आपको एक आयताकार की किन्हीं दो भुजाओं की लंबाई जानने की आवश्यकता है त्रिकोण .

2. यदि स्थितियाँ पैरों के आयाम निर्दिष्ट करती हैं, तो कर्ण की लंबाई ज्ञात करें। ऐसा करने के लिए, कैलकुलेटर का उपयोग करके, पैरों के योग का वर्गमूल निकालें, उनमें से प्रत्येक का पहले से वर्ग करें।

3. यदि आप कर्ण और दूसरे पैर के आयाम जानते हैं तो एक पैर की लंबाई की गणना करें। कैलकुलेटर का उपयोग करके, कर्ण के वर्ग और अग्रणी पैर के वर्ग के बीच के अंतर का वर्गमूल निकालें।

4. यदि समस्या कर्ण और उसके निकटवर्ती तीव्र कोणों में से एक को निर्दिष्ट करती है, तो ब्रैडिस तालिकाओं का उपयोग करें। वे बड़ी संख्या में कोणों के लिए त्रिकोणमितीय कार्यों के मान प्रदान करते हैं। साइन और कोसाइन फ़ंक्शंस के साथ-साथ त्रिकोणमिति प्रमेयों के साथ एक कैलकुलेटर का उपयोग करें जो एक आयताकार के पक्षों और कोणों के बीच संबंधों का वर्णन करता है त्रिकोण .

5. बुनियादी त्रिकोणमितीय कार्यों का उपयोग करके पैर खोजें: a = c*sin?, b = c*cos?, जहां a कोने के विपरीत पैर है?, b कोने से सटा हुआ पैर है? इसी प्रकार भुजाओं के आकार की गणना करें त्रिकोण, यदि कर्ण और एक अन्य न्यून कोण दिया गया है: b = c*sin?, a = c*cos?, जहां b कोण के विपरीत पैर है?, और क्या पैर कोण के निकट है?

6. उस स्थिति में जब हम पैर a और उससे सटे न्यून कोण को लेते हैं?, यह न भूलें कि एक समकोण त्रिभुज में न्यून कोणों का योग हमेशा 90° के बराबर होता है: ? + ? = 90°. पैर a के विपरीत कोण का मान ज्ञात कीजिए: ? = 90° – ?. या त्रिकोणमितीय कमी सूत्रों का उपयोग करें: पाप? = पाप (90° – ?) = क्योंकि ?; टीजी? = टीजी (90° – ?) = सीटीजी ? = 1/टीजी?

7. यदि हमारे पास पाद a है और इसके विपरीत तीव्र कोण है?, ब्रैडिस तालिकाओं, एक कैलकुलेटर और त्रिकोणमितीय कार्यों का उपयोग करके, सूत्र का उपयोग करके कर्ण की गणना करें: c=a*sin?, पाद: b=a*tg?।

विषय पर वीडियो

त्रिभुज की मध्य रेखा की अवधारणा

आइए हम त्रिभुज की मध्य रेखा की अवधारणा का परिचय दें।

परिभाषा 1

यह एक त्रिभुज की दो भुजाओं के मध्य बिंदुओं को जोड़ने वाला एक खंड है (चित्र 1)।

चित्र 1. त्रिभुज की मध्य रेखा

त्रिभुज मध्य रेखा प्रमेय

प्रमेय 1

किसी त्रिभुज की मध्य रेखा उसकी एक भुजा के समानांतर और उसके आधे भाग के बराबर होती है।

सबूत।

आइए हमें एक त्रिभुज $ABC$ दिया जाए। $MN$ मध्य रेखा है (जैसा कि चित्र 2 में है)।

चित्र 2. प्रमेय 1 का चित्रण

चूँकि $\frac(AM)(AB)=\frac(BN)(BC)=\frac(1)(2)$, तो त्रिभुज $ABC$ और $MBN$ त्रिभुजों की समानता के दूसरे मानदंड के अनुसार समान हैं . मतलब

साथ ही, यह इस प्रकार है कि $\कोण A=\कोण BMN$, जिसका अर्थ है $MN||AC$।

प्रमेय सिद्ध हो चुका है।

त्रिभुज मध्य रेखा प्रमेय के परिणाम

परिणाम 1:एक त्रिभुज की माध्यिकाएं एक बिंदु पर प्रतिच्छेद करती हैं और शीर्ष से प्रारंभ करके प्रतिच्छेदन बिंदु द्वारा $2:1$ के अनुपात में विभाजित होती हैं।

सबूत।

त्रिभुज $ABC$ पर विचार करें, जहां $(AA)_1,\ (BB)_1,\ (CC)_1$ इसकी माध्यिकाएं हैं। चूँकि माध्यिकाएँ भुजाओं को आधे में विभाजित करती हैं। आइए मध्य रेखा $A_1B_1$ पर विचार करें (चित्र 3)।

चित्र 3. परिणाम 1 का चित्रण

प्रमेय 1 के अनुसार, $AB||A_1B_1$ और $AB=2A_1B_1$, इसलिए, $\कोण ABB_1=\कोण BB_1A_1,\ \कोण BAA_1=\कोण AA_1B_1$। इसका मतलब यह है कि त्रिकोण $ABM$ और $A_1B_1M$ त्रिकोणों की समानता के पहले मानदंड के अनुसार समान हैं। तब

इसी प्रकार यह भी सिद्ध हो गया है

प्रमेय सिद्ध हो चुका है।

परिणाम 2:त्रिभुज की तीन मध्य रेखाएँ इसे समानता गुणांक $k=\frac(1)(2)$ के साथ मूल त्रिभुज के समान 4 त्रिभुजों में विभाजित करती हैं।

सबूत।

मध्य रेखाओं $A_1B_1,\ (\ A)_1C_1,\ B_1C_1$ वाले त्रिभुज $ABC$ पर विचार करें (चित्र 4)

चित्र 4. परिणाम 2 का चित्रण

त्रिभुज $A_1B_1C$ पर विचार करें। चूँकि $A_1B_1$ मध्य रेखा है, तो

कोण $C$ इन त्रिभुजों का उभयनिष्ठ कोण है। नतीजतन, त्रिकोण $A_1B_1C$ और $ABC$ समानता गुणांक $k=\frac(1)(2)$ वाले त्रिकोणों की समानता के दूसरे मानदंड के अनुसार समान हैं।

इसी तरह, यह साबित हो गया है कि त्रिकोण $A_1C_1B$ और $ABC$, और त्रिकोण $C_1B_1A$ और $ABC$ समानता गुणांक $k=\frac(1)(2)$ के साथ समान हैं।

त्रिभुज $A_1B_1C_1$ पर विचार करें। चूँकि $A_1B_1,\ (\A)_1C_1,\ B_1C_1$ त्रिभुज की मध्य रेखाएँ हैं, तो

इसलिए, त्रिभुजों की समानता के तीसरे मानदंड के अनुसार, त्रिभुज $A_1B_1C_1$ और $ABC$ समानता गुणांक $k=\frac(1)(2)$ के साथ समान हैं।

प्रमेय सिद्ध हो चुका है।

त्रिभुज की मध्य रेखा की अवधारणा पर समस्याओं के उदाहरण

उदाहरण 1

$16$ सेमी, $10$ सेमी और $14$ सेमी भुजाओं वाला एक त्रिभुज दिया गया है। उस त्रिभुज का परिमाप ज्ञात कीजिए जिसके शीर्ष दिए गए त्रिभुज की भुजाओं के मध्य बिंदु पर स्थित हैं।

समाधान।

चूँकि वांछित त्रिभुज के शीर्ष दिए गए त्रिभुज की भुजाओं के मध्य बिंदुओं पर स्थित हैं, तो इसकी भुजाएँ मूल त्रिभुज की मध्य रेखाएँ हैं। परिणाम 2 से, हम पाते हैं कि वांछित त्रिभुज की भुजाएँ $8$ सेमी, $5$ सेमी और $7$ सेमी के बराबर हैं।

उत्तर:$20$ देखें

उदाहरण 2

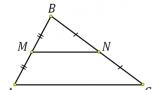
एक त्रिभुज $ABC$ दिया गया है। बिंदु $N\ और\ M$ क्रमशः $BC$ और $AB$ भुजाओं के मध्यबिंदु हैं (चित्र 5)।

चित्र 5.

त्रिभुज $BMN=14$ सेमी का परिमाप। त्रिभुज $ABC$ का परिमाप ज्ञात कीजिए।

समाधान।

चूँकि $N\ और\ M$ भुजाओं $BC$ और $AB$ के मध्यबिंदु हैं, तो $MN$ मध्य रेखा है। मतलब

प्रमेय 1 के अनुसार, $AC=2MN$। हम पाते हैं:

\[(\बड़ा(\पाठ(त्रिभुजों की समानता)))\]

परिभाषाएं

दो त्रिभुज समरूप कहलाते हैं यदि उनके कोण क्रमशः बराबर हों और एक त्रिभुज की भुजाएँ दूसरे त्रिभुज की समरूप भुजाओं के समानुपाती हों
(यदि भुजाएँ समान कोणों के विपरीत स्थित हों तो उन्हें समरूप कहा जाता है)।

(समान) त्रिभुजों की समानता का गुणांक इन त्रिभुजों की समान भुजाओं के अनुपात के बराबर एक संख्या है।

परिभाषा

किसी त्रिभुज का परिमाप उसकी सभी भुजाओं की लंबाई का योग होता है।

प्रमेय

दो समरूप त्रिभुजों की परिमापों का अनुपात समरूपता गुणांक के बराबर होता है।

सबूत

क्रमशः \(a,b,c\) और \(a_1, b_1, c_1\) भुजाओं वाले त्रिभुजों \(ABC\) और \(A_1B_1C_1\) पर विचार करें (ऊपर चित्र देखें)।

तब \(P_(ABC)=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_(A_1B_1C_1)\)

प्रमेय

दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात समरूपता गुणांक के वर्ग के बराबर होता है।

सबूत

मान लीजिए कि त्रिभुज \(ABC\) और \(A_1B_1C_1\) समरूप हैं, और \(\dfrac(AB)(A_1B_1) = \dfrac(AC)(A_1C_1) = \dfrac(BC)(B_1C_1) = k\). आइए इन त्रिभुजों के क्षेत्रफलों को क्रमशः \(S\) और \(S_1\) अक्षरों से निरूपित करें।

चूँकि \(\कोण A = \कोण A_1\) , तो \(\dfrac(S)(S_1) = \dfrac(AB\cdot AC)(A_1B_1\cdot A_1C_1)\)(समान कोणों वाले त्रिभुजों के क्षेत्रफलों के अनुपात पर प्रमेय के अनुसार)।

क्योंकि \(\dfrac(AB)(A_1B_1) = \dfrac(AC)(A_1C_1) = k\), वह \(\dfrac(S)(S_1) = \dfrac(AB)(A_1B_1)\cdot\dfrac(AC)(A_1C_1) = k\cdot k = k^2\), जिसे सिद्ध करने की आवश्यकता थी।

\[(\बड़ा(\पाठ(त्रिभुजों की समानता के चिह्न)))\]

प्रमेय (त्रिकोणों की समानता का पहला संकेत)

यदि एक त्रिभुज के दो कोण क्रमशः दूसरे त्रिभुज के दो कोणों के बराबर हों, तो ऐसे त्रिभुज समरूप होते हैं।

सबूत

मान लीजिए \(ABC\) और \(A_1B_1C_1\) इस प्रकार त्रिभुज हैं कि \(\कोण A = \कोण A_1\) , \(\कोण B = \कोण B_1\) । फिर, त्रिभुज के कोणों के योग पर प्रमेय द्वारा \(\कोण C = 180^\circ - \कोण A - \कोण B = 180^\circ - \कोण A_1 - \कोण B_1 = \कोण C_1\), अर्थात्, त्रिभुज \(ABC\) के कोण क्रमशः त्रिभुज \(A_1B_1C_1\) के कोणों के बराबर हैं।

चूँकि \(\कोण A = \कोण A_1\) और \(\कोण B = \कोण B_1\) , तो \(\dfrac(S_(ABC))(S_(A_1B_1C_1)) = \dfrac(AB\cdot AC)(A_1B_1\cdot A_1C_1)\)और \(\dfrac(S_(ABC))(S_(A_1B_1C_1)) = \dfrac(AB\cdot BC)(A_1B_1\cdot B_1C_1)\).

इन समानताओं से यह निष्कर्ष निकलता है \(\dfrac(AC)(A_1C_1) = \dfrac(BC)(B_1C_1)\).

इसी प्रकार यह भी सिद्ध हो गया है \(\dfrac(AC)(A_1C_1) = \dfrac(AB)(A_1B_1)\)(समानताओं का उपयोग करते हुए \(\कोण B = \कोण B_1\) , \(\कोण C = \कोण C_1\) ).

परिणामस्वरूप, त्रिभुज \(ABC\) की भुजाएँ त्रिभुज \(A_1B_1C_1\) की समान भुजाओं के समानुपाती होती हैं, जिसे सिद्ध करने की आवश्यकता है।

प्रमेय (त्रिकोणों की समानता के लिए दूसरा मानदंड)

यदि एक त्रिभुज की दो भुजाएँ दूसरे त्रिभुज की दो भुजाओं के समानुपाती हों और इन भुजाओं के बीच के कोण बराबर हों, तो त्रिभुज समरूप होते हैं।

सबूत

ऐसे दो त्रिभुजों \(ABC\) और \(A"B"C"\) पर विचार करें \(\dfrac(AB)(A"B")=\dfrac(AC)(A"C")\), \(\कोण BAC = \कोण A"\) आइए सिद्ध करें कि त्रिभुज \(ABC\) और \(A"B"C"\) समरूप हैं। त्रिभुजों की समानता के पहले चिह्न को ध्यान में रखते हुए, यह दर्शाने के लिए पर्याप्त है कि \(\कोण B = \कोण B"\) ।

\(\कोण 1 = \कोण A"\) , \(\कोण 2 = \कोण B"\) वाले एक त्रिभुज \(ABC""\) पर विचार करें। त्रिभुजों की समानता की पहली कसौटी के अनुसार त्रिभुज \(ABC""\) और \(A"B"C"\) समान हैं, तो \(\dfrac(AB)(A"B") = \dfrac(AC"")(A"C")\).

दूसरी ओर, शर्त से \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C")\). अंतिम दो समानताओं से यह निष्कर्ष निकलता है कि \(AC = AC""\) ।

त्रिभुज \(ABC\) और \(ABC""\) की दो भुजाएँ और उनके बीच का कोण बराबर है, इसलिए, \(\कोण बी = \कोण 2 = \कोण बी"\).

प्रमेय (त्रिकोणों की समानता का तीसरा चिह्न)

यदि एक त्रिभुज की तीन भुजाएँ दूसरे त्रिभुज की तीन भुजाओं के समानुपाती हों, तो त्रिभुज समरूप होते हैं।

सबूत

माना त्रिभुजों \(ABC\) और \(A"B"C"\) की भुजाएँ आनुपातिक हैं: \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C") = \dfrac(BC)(B"C")\). आइए हम सिद्ध करें कि त्रिभुज \(ABC\) और \(A"B"C"\) समरूप हैं।

ऐसा करने के लिए, त्रिभुजों की समानता के लिए दूसरे मानदंड को ध्यान में रखते हुए, यह साबित करना पर्याप्त है कि \(\कोण BAC = \कोण A"\) ।

\(\कोण 1 = \कोण A"\) , \(\कोण 2 = \कोण B"\) वाले एक त्रिभुज \(ABC""\) पर विचार करें।

त्रिभुजों की समानता की पहली कसौटी के अनुसार त्रिभुज \(ABC""\) और \(A"B"C"\) समान हैं, इसलिए, \(\dfrac(AB)(A"B") = \dfrac(BC"")(B"C") = \dfrac(C""A)(C"A")\).

समानताओं और स्थितियों की अंतिम श्रृंखला से \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C") = \dfrac(BC)(B"C")\)यह इस प्रकार है कि \(BC = BC""\) , \(CA = C""A\) ।

त्रिभुज \(ABC\) और \(ABC""\) तीन भुजाओं पर बराबर हैं, इसलिए, \(\कोण बीएसी = \कोण 1 = \कोण ए"\).

\[(\बड़ा(\पाठ(थेल्स प्रमेय)))\]

प्रमेय

यदि आप किसी कोण के एक तरफ समान खंडों को चिह्नित करते हैं और उनके सिरों से समानांतर सीधी रेखाएं खींचते हैं, तो ये सीधी रेखाएं दूसरी तरफ भी समान खंडों को काट देंगी।

सबूत

आइए पहले साबित करें लेम्मा:यदि \(\त्रिकोण OBB_1\) में भुजा \(OB\) के मध्य \(A\) से होकर एक सीधी रेखा \(a\समानांतर BB_1\) खींची जाती है, तो यह भुजा \(OB_1\) को भी प्रतिच्छेद करेगी मध्य।

बिंदु \(B_1\) से होकर हम \(l\समानांतर OB\) खींचते हैं। चलो \(l\cap a=K\) । तब \(ABB_1K\) एक समांतर चतुर्भुज है, इसलिए \(B_1K=AB=OA\) और \(\कोण A_1KB_1=\कोण ABB_1=\कोण OAA_1\); \(\कोण AA_1O=\कोण KA_1B_1\)ऊर्ध्वाधर की तरह. तो, दूसरे संकेत के अनुसार \(\त्रिकोण OAA_1=\त्रिकोण B_1KA_1 \दायां तीर OA_1=A_1B_1\). लेम्मा सिद्ध है.

आइए प्रमेय के प्रमाण की ओर आगे बढ़ें। मान लीजिए \(OA=AB=BC\) , \(a\parallel b\parallel c\) और हमें यह साबित करने की जरूरत है कि \(OA_1=A_1B_1=B_1C_1\) ।

इस प्रकार, इस प्रमेयिका \(OA_1=A_1B_1\) के अनुसार। आइए साबित करें कि \(A_1B_1=B_1C_1\) । आइए बिंदु \(B_1\) से होकर एक रेखा \(d\parallel OC\) खींचें, और मान लें कि \(d\cap a=D_1, d\cap c=D_2\) । तब \(ABB_1D_1, BCD_2B_1\) समांतर चतुर्भुज हैं, इसलिए, \(D_1B_1=AB=BC=B_1D_2\) । इस प्रकार, \(\कोण A_1B_1D_1=\कोण C_1B_1D_2\)ऊर्ध्वाधर की तरह \(\कोण A_1D_1B_1=\कोण C_1D_2B_1\)क्रॉस की तरह झूठ बोलना, और इसलिए, दूसरे संकेत के अनुसार \(\त्रिकोण A_1B_1D_1=\त्रिकोण C_1B_1D_2 \दायां तीर A_1B_1=B_1C_1\).

थेल्स का प्रमेय

समानांतर रेखाएं किसी कोण के किनारों पर आनुपातिक खंडों को काटती हैं।

सबूत

चलो समानांतर रेखाएँ \(p\समानांतर q\समानांतर r\समानांतर s\)एक पंक्ति को खंडों \(a, b, c, d\) में विभाजित किया। फिर दूसरी सीधी रेखा को क्रमशः खंडों \(ka, kb, kc, kd\) में विभाजित किया जाना चाहिए, जहां \(k\) एक निश्चित संख्या है, खंडों का समान आनुपातिक गुणांक है।

आइए बिंदु \(A_1\) से होकर एक रेखा \(p\parallel OD\) खींचें (\(ABB_2A_1\) एक समांतर चतुर्भुज है, इसलिए, \(AB=A_1B_2\) )। तब \(\त्रिकोण OAA_1 \सिम \त्रिकोण A_1B_1B_2\)दो कोनों पर. इस तरह, \(\dfrac(OA)(A_1B_2)=\dfrac(OA_1)(A_1B_1) \राइटएरो A_1B_1=kb\).

इसी प्रकार, हम \(B_1\) से होकर एक सीधी रेखा खींचते हैं \(q\समानांतर OD \दायां तीर \त्रिकोण OBB_1\sim \त्रिकोण B_1C_1C_2 \दायां तीर B_1C_1=kc\)वगैरह।

\[(\बड़ा(\पाठ(त्रिभुज की मध्य रेखा)))\]

परिभाषा

त्रिभुज की मध्य रेखा त्रिभुज की किन्हीं दो भुजाओं के मध्य बिंदुओं को जोड़ने वाला एक खंड है।

प्रमेय

त्रिभुज की मध्य रेखा तीसरी भुजा के समानांतर और उसके आधे भाग के बराबर होती है।

सबूत

1) मध्य रेखा से आधार की समानता ऊपर सिद्ध की गई बातों के अनुरूप है लेम्मास.

2) आइए हम साबित करें कि \(MN=\dfrac12 AC\) ।

बिंदु \(N\) से होकर हम \(AB\) के समानांतर एक रेखा खींचते हैं। मान लीजिए कि यह रेखा भुजा \(AC\) को बिंदु \(K\) पर काटती है। तब \(AMNK\) एक समांतर चतुर्भुज है ( \(AM\समानांतर NK, MN\समानांतर AK\)पिछले बिंदु के अनुसार)। तो, \(MN=AK\) ।

क्योंकि \(NK\parallel AB\) और \(N\) \(BC\) का मध्यबिंदु है, तो थेल्स प्रमेय के अनुसार \(K\) \(AC\) का मध्यबिंदु है। इसलिए, \(MN=AK=KC=\dfrac12 AC\) ।

परिणाम

त्रिभुज की मध्य रेखा दिए गए त्रिभुज के समान गुणांक \(\frac12\) से काटती है।

1 अतिरिक्त निर्माण जो त्रिभुज मध्य रेखा प्रमेय, समलम्बाकार और त्रिभुजों की समानता गुणों की ओर ले जाता है।

और वह आधे कर्ण के बराबर.
परिणाम 1.
परिणाम 2.

इससे यह स्पष्ट है कि

1 समान न्यूनकोण वाले सभी समकोण त्रिभुज समरूप होते हैं। त्रिकोणमितीय कार्यों पर एक नजर.

रची हुई और बिना रची हुई भुजाओं वाले त्रिभुज समान होते हैं क्योंकि उनके दोनों कोण बराबर होते हैं। इसलिए कहां

इसका मतलब यह है कि संकेतित संबंध केवल समकोण त्रिभुज के न्यून कोण पर निर्भर करते हैं और अनिवार्य रूप से इसे निर्धारित करते हैं। यह त्रिकोणमितीय कार्यों की उपस्थिति के कारणों में से एक है:

अक्सर समान समकोण त्रिभुजों में कोणों के त्रिकोणमितीय फलन लिखना समरूपता संबंध लिखने की तुलना में अधिक स्पष्ट होता है!

आइए हम ऊँचाई CH को कर्ण AB से कम करें। हमारे पास तीन समरूप त्रिभुज ABC, AHC और CHB हैं। आइए त्रिकोणमितीय फलनों के लिए व्यंजक लिखें:

इससे यह स्पष्ट है कि . जोड़ने पर, हमें पाइथागोरस प्रमेय प्राप्त होता है, क्योंकि:

पाइथागोरस प्रमेय के एक अन्य प्रमाण के लिए, समस्या 4 की टिप्पणी देखें।
3 अतिरिक्त निर्माण का एक महत्वपूर्ण उदाहरण त्रिभुज के किसी एक कोण के बराबर कोण का निर्माण है।

समकोण के शीर्ष से हम एक सीधी रेखा खंड खींचते हैं जो दिए गए समकोण त्रिभुज ABC के कोण CAB के बराबर पाद CA के साथ एक कोण बनाता है। परिणामस्वरूप, हमें आधार कोणों वाला एक समद्विबाहु त्रिभुज ACM प्राप्त होता है। लेकिन इस निर्माण से उत्पन्न होने वाला दूसरा त्रिभुज भी समद्विबाहु होगा, क्योंकि आधार पर इसका प्रत्येक कोण बराबर है (एक समकोण त्रिभुज के कोणों की संपत्ति और निर्माण द्वारा - कोण को समकोण से "घटाया" गया था)। इस तथ्य के कारण कि त्रिभुज बीएमसी और एएमसी उभयनिष्ठ भुजा एमसी के साथ समद्विबाहु हैं, हमारे पास समानता एमबी=एमए=एमसी है, यानी। एम.सी. एक समकोण त्रिभुज के कर्ण पर खींची गई माध्यिका, और वह आधे कर्ण के बराबर.
परिणाम 1.कर्ण का मध्यबिंदु इस त्रिभुज के चारों ओर परिचालित वृत्त का केंद्र है, क्योंकि इससे पता चलता है कि कर्ण का मध्यबिंदु समकोण त्रिभुज के शीर्षों से समान दूरी पर है।
परिणाम 2.एक समकोण त्रिभुज की मध्य रेखा, कर्ण के मध्य और पैर के मध्य को जोड़ती है, विपरीत पैर के समानांतर होती है और उसके आधे के बराबर होती है।

समद्विबाहु त्रिभुज बीएमसी और एएमसी में, आइए हम एमएच और एमजी की ऊंचाई को आधार से कम करें। चूँकि एक समद्विबाहु त्रिभुज में, आधार से नीचे की ऊँचाई भी माध्यिका (और समद्विभाजक) होती है, तो MH और MG एक समकोण त्रिभुज की रेखाएँ हैं जो कर्ण के मध्य को पैरों के मध्य बिंदुओं से जोड़ती हैं। निर्माण से, वे विपरीत पैरों के समानांतर और उनके आधे के बराबर हो जाते हैं, क्योंकि त्रिकोण बराबर हैं एमएचसी और एमजीसी बराबर हैं (और एमएचसीजी एक आयत है)। यह परिणाम एक मनमाना त्रिभुज की मध्य रेखा पर प्रमेय के प्रमाण का आधार है और, आगे, एक ट्रेपेज़ॉइड की मध्य रेखा और उन्हें प्रतिच्छेद करने वाली दो सीधी रेखाओं पर समानांतर रेखाओं द्वारा काटे गए खंडों की आनुपातिकता की संपत्ति है।

कार्य
समानता गुणों का उपयोग -1
मूल गुणों का उपयोग - 2
अतिरिक्त गठन का उपयोग 3-4

1 2 3 4

एक समकोण त्रिभुज के समकोण के शीर्ष से गिराई गई ऊंचाई उन खंडों की लंबाई के वर्गमूल के बराबर होती है जिनमें यह कर्ण को विभाजित करता है।

यदि आप त्रिभुजों की समानता से पाइथागोरस प्रमेय की व्युत्पत्ति जानते हैं तो समाधान स्पष्ट प्रतीत होता है:

\(\mathrm(tg)\beta=\frac(h)(c_1)=\frac(c_2)(h)\),
जहां से \(h^2=c_1c_2\).

उन सभी संभावित समकोण त्रिभुजों की माध्यिकाओं के प्रतिच्छेदन बिंदु (GMT) का स्थान ज्ञात कीजिए जिनका कर्ण AB निश्चित है।

किसी भी त्रिभुज की माध्यिकाओं का प्रतिच्छेदन बिंदु, संगत भुजा के साथ उसके प्रतिच्छेदन बिंदु से गिनती करते हुए, माध्यिका से एक तिहाई काट देता है। एक समकोण त्रिभुज में, समकोण से खींची गई माध्यिका कर्ण के आधे के बराबर होती है। इसलिए, वांछित GMT कर्ण की लंबाई के 1/6 के बराबर त्रिज्या का एक वृत्त है, जिसमें इस (निश्चित) कर्ण के मध्य में एक केंद्र होता है।