जड़ता का घूर्णी गति क्षण. विषय ii. जड़ता बल. किसी कठोर पिंड की घूर्णी गति. शक्ति का क्षण
जटिल गतिविधियों, जैसे कि मानव शरीर की गति (चलना, दौड़ना, कूदना आदि) का अवलोकन करते समय, इसके सभी बिंदुओं की गति का वर्णन करना कठिन या असंभव भी लगता है। हालाँकि, ऐसे आंदोलनों का विश्लेषण करते हुए, कोई यह देख सकता है कि उनमें सरल - अनुवादात्मक और घूर्णी आंदोलन शामिल हैं।
अनुवादकीय गति की यांत्रिकी पाठक को ज्ञात है, इसलिए यह अनुभाग घूर्णी गति के विचार से शुरू होता है। सबसे सरल है एक कठोर पिंड का एक निश्चित अक्ष के चारों ओर घूमना। यह मामला आपको घूर्णी गति की विशिष्टताओं, शब्दावली और नियमों से परिचित होने की अनुमति देता है।
5.1. एक निश्चित अक्ष के चारों ओर एक बिल्कुल कठोर शरीर की घूर्णी गति की गतिकी
पूर्णतः कठोर पिंड वह है जिसके किन्हीं दो बिंदुओं के बीच की दूरी स्थिर होती है।
बिल्कुल कठोर पिंड के हिलने पर उसके आयाम और आकार नहीं बदलते हैं।
"बिल्कुल कठोर शरीर" की अवधारणा एक भौतिक अमूर्तता है, क्योंकि कोई भी शरीर विरूपण में सक्षम है। हालाँकि, कई मामलों में विकृति को नजरअंदाज किया जा सकता है।
किसी बिल्कुल कठोर पिंड की घूर्णी गति का सबसे सरल मामला एक निश्चित अक्ष के चारों ओर घूमना है। यह एक गति है जिसमें शरीर के बिंदु वृत्तों में घूमते हैं, जिनके केंद्र एक सीधी रेखा पर स्थित होते हैं, जिसे घूर्णन की धुरी कहा जाता है।
यह ज्ञात है कि कुछ मामलों में, किसी पिंड की गति को चिह्नित करने के लिए, उसके सभी बिंदुओं की गति को इंगित करना आवश्यक नहीं है; इसलिए, उदाहरण के लिए, अनुवादात्मक गति में यह शरीर के किसी एक बिंदु की गति को इंगित करने के लिए पर्याप्त है।
एक अक्ष के चारों ओर घूर्णी गति के दौरान, शरीर के बिंदु विभिन्न प्रक्षेप पथों के साथ चलते हैं, लेकिन एक ही समय के दौरान, सभी बिंदु और शरीर स्वयं एक ही कोण पर घूमते हैं। घूर्णन विशेषताओं के लिए
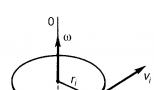
अक्ष के लंबवत समतल में एक निश्चित बिंदु पर त्रिज्या वेक्टर बनाएं मैं(चित्र 5.1)। कुछ चयनित दिशा OX के सापेक्ष त्रिज्या वेक्टर के घूर्णन के कोण α की समय निर्भरता एक निश्चित अक्ष के चारों ओर एक कठोर शरीर की घूर्णी गति का समीकरण है:
किसी पिंड के घूमने की गति को समय के संबंध में त्रिज्या वेक्टर के रोटेशन के कोण के पहले व्युत्पन्न के बराबर कोणीय वेग द्वारा दर्शाया जाता है:
कोणीय वेग एक सदिश है जो घूर्णन अक्ष के अनुदिश निर्देशित होता है और दाएं पेंच के नियम द्वारा घूर्णन की दिशा से संबंधित होता है (चित्र 5.2)। कोणीय वेग वेक्टर, वेग और बल वैक्टर के विपरीत, फिसल रहा है: इसमें आवेदन का एक विशिष्ट बिंदु नहीं है, और यह रोटेशन अक्ष पर कहीं भी स्थित हो सकता है। इस प्रकार, वेक्टर को निर्दिष्ट करना घूर्णन अक्ष की स्थिति, घूर्णन की दिशा और कोणीय वेग के परिमाण को इंगित करता है।

कोणीय वेग में परिवर्तन की दर को समय के संबंध में कोणीय वेग के पहले व्युत्पन्न के बराबर कोणीय त्वरण द्वारा दर्शाया जाता है:
या वेक्टर रूप में:
(5.4) से यह स्पष्ट है कि कोणीय त्वरण वेक्टर, कोणीय वेग वेक्टर dω में एक प्रारंभिक, बल्कि छोटे परिवर्तन के साथ दिशा में मेल खाता है: त्वरित घूर्णन के साथ, कोणीय त्वरण कोणीय वेग के समान दिशा में निर्देशित होता है, धीमी गति से घूमने पर - विपरीत दिशा में।
चूँकि एक बिल्कुल कठोर पिंड के सभी बिंदुओं का कोणीय विस्थापन समान होता है, तो, (5.2) और (5.3) के अनुसार, एक ही समय में शरीर के सभी बिंदुओं का कोणीय वेग और कोणीय त्वरण समान होता है। रैखिक विशेषताएँ - विस्थापन, गति, त्वरण - अलग-अलग बिंदुओं के लिए अलग-अलग हैं। आइए हम त्रिज्या के एक वृत्त में घूमने वाले i-वें बिंदु के लिए रैखिक और कोणीय विशेषताओं के बीच संबंध को अदिश रूप में इंगित करें, जिसे स्वतंत्र रूप से प्राप्त किया जा सकता है। आर मैं:

चावल। 5.3

अंत में, हम संबंधित अभिव्यक्तियों को एकीकृत करके प्राप्त एक निश्चित अक्ष के चारों ओर एक कठोर शरीर की घूर्णी गति की गतिकी के लिए सूत्र प्रस्तुत करते हैं:
एकसमान घूर्णी गति का समीकरण[सेमी। (5.2)]:
एकसमान घूर्णी गति में समय पर कोणीय वेग की निर्भरता[सेमी। (5.3)]:
समान रूप से वैकल्पिक घूर्णी गति का समीकरण[सेमी। (5.1) और (5.6)]:
अनुवादात्मक गति के लिए समान निर्भरताओं के साथ इन सूत्रों की तुलना करना उपयोगी है।
5.2. बुनियादी अवधारणाओं। घूर्णी गति की गतिशीलता के लिए समीकरण
शक्ति का क्षण_
चलो कुछ बिंदु पर मैंकिसी कठोर पिंड पर लगाया गया बल एफ^,घूर्णन अक्ष के लंबवत समतल में स्थित (चित्र 5.4)।
घूर्णन अक्ष के सापेक्ष बल का क्षण बिंदु i की त्रिज्या वेक्टर और बल का वेक्टर उत्पाद है:
इसका विस्तार करते हुए आप लिख सकते हैं:
कहाँ β - सदिशों के बीच का कोण आर मैंऔर एफ मैं .बल के कंधे के बाद से एच आई = आर आईफिर, पापβ (चित्र 5.4 देखें)।
यदि बल घूर्णन तल पर एक निश्चित कोण α पर कार्य करता है (चित्र 5.5), तो इसे दो घटकों में विघटित किया जा सकता है। उनमें से एक रोटेशन की धुरी के लंबवत विमान में स्थित है, और दूसरा इस धुरी के समानांतर है और शरीर के घूर्णन को प्रभावित नहीं करता है (वास्तविक मामले में, यह केवल बीयरिंग पर कार्य करता है)। इसके अलावा, केवल घूर्णन अक्ष के लंबवत तल में स्थित बलों पर ही विचार किया जाएगा।

चावल। 5.4

चावल। 5.5
घूर्णी गति में कार्य करें
बल की कार्रवाई के तहत चलो एफ मैं(चित्र 5.4 देखें) शरीर पर्याप्त रूप से छोटे कोण dα से घूमता है। आइये इस बल द्वारा किया गया कार्य ज्ञात करें।
इस मामले में हाई स्कूल से ज्ञात बल के कार्य की अभिव्यक्ति इस प्रकार लिखी जानी चाहिए:

इसलिए,
घूर्णी गति में बल का प्राथमिक कार्य बल के क्षण और पिंड के घूर्णन के प्रारंभिक कोण के उत्पाद के बराबर होता है।
यदि किसी पिंड पर कई बल कार्य करते हैं, तो उन सभी द्वारा किया गया प्रारंभिक कार्य इसी प्रकार निर्धारित किया जाता है (5.12):
कहाँ एम- शरीर पर कार्य करने वाली सभी बाहरी शक्तियों का कुल क्षण।
यदि, जब पिंड घूमता है, तो त्रिज्या वेक्टर की स्थिति α 1 से α 2 में बदल जाती है, तो बाहरी बलों का कार्य अभिव्यक्ति (5.13) को एकीकृत करके पाया जा सकता है:
निष्क्रियता के पल
स्थानांतरीय गति के दौरान पिंडों की जड़ता का माप द्रव्यमान है। घूर्णी गति के दौरान पिंडों की जड़ता न केवल द्रव्यमान पर निर्भर करती है, बल्कि अक्ष के सापेक्ष अंतरिक्ष में इसके वितरण पर भी निर्भर करती है। घूर्णन के दौरान किसी पिंड की जड़ता का माप घूर्णन के अक्ष के सापेक्ष पिंड की जड़ता के क्षण से निर्धारित होता है। आइए सबसे पहले हम उस पर ध्यान दें
घूर्णन अक्ष के सापेक्ष किसी भौतिक बिंदु की जड़ता का क्षण, अक्ष से उसकी दूरी के वर्ग द्वारा बिंदु के द्रव्यमान के गुणनफल के बराबर होता है:
किसी अक्ष के सापेक्ष किसी पिंड की जड़ता का क्षण शरीर को बनाने वाले सभी भौतिक बिंदुओं की जड़ता के क्षणों का योग है:


उदाहरण के तौर पर हम सूत्र निकालते हैं एक पतली सजातीय छड़ का जड़त्व आघूर्णलंबाई एलऔर द्रव्यमान टीछड़ के लंबवत और उसके मध्य से गुजरने वाली धुरी के सापेक्ष (चित्र 5.6)। आइए हम लंबाई के साथ छड़ का एक पर्याप्त छोटा खंड चुनें डीएक्सऔर द्रव्यमान डीएम,अक्ष 00" से दूरी पर है एक्स।इस क्षेत्र के छोटे होने के कारण, इसे एक भौतिक बिंदु, इसकी जड़ता के क्षण के रूप में लिया जा सकता है [देखें। (5.15)] इसके बराबर है:
प्रारंभिक खंड का द्रव्यमान रैखिक घनत्व के उत्पाद के बराबर है टी/एल,प्रारंभिक अनुभाग की लंबाई से गुणा किया गया: डी.एम= (m/l) dx इस व्यंजक को (5.18) में प्रतिस्थापित करने पर, हमें प्राप्त होता है
संपूर्ण छड़ का जड़त्व आघूर्ण ज्ञात करने के लिए, हम अभिव्यक्ति (5.19) को संपूर्ण छड़ पर एकीकृत करते हैं, अर्थात। -1/2 से +1/2 तक:

आइए हम द्रव्यमान के विभिन्न सममित निकायों की जड़ता के क्षणों के लिए अभिव्यक्ति प्रस्तुत करें टी:
खोखला सजातीय सिलेंडर(घेरा) आंतरिक त्रिज्या के साथ आरऔर बाहरी आरअक्ष OO" के सापेक्ष, सिलेंडर के ज्यामितीय अक्ष के साथ मेल खाता है (चित्र 5.7):
निरंतर सजातीय सिलेंडर (आर = 0) या डिस्क [देखें (5.21)]:
सजातीय गेंद इसके केंद्र से गुजरने वाली धुरी के सापेक्ष:
आयताकार समांतर चतुर्भुज आधार के तल के लंबवत इसके केंद्र से गुजरने वाली धुरी OO" के सापेक्ष (चित्र 5.8):
उपरोक्त सभी उदाहरणों में, घूर्णन की धुरी पिंड के द्रव्यमान के केंद्र से होकर गुजरती है। द्रव्यमान के केंद्र से नहीं गुजरने वाली धुरी के बारे में किसी पिंड की जड़ता के क्षण को निर्धारित करने के लिए समस्याओं को हल करते समय, आप ह्यूजेन्स प्रमेय का उपयोग कर सकते हैं। इस प्रमेय के अनुसार, किसी अक्ष OO के सापेक्ष पिंड की जड़ता का क्षण:
जहां J 0 पिंड के द्रव्यमान केंद्र OO से गुजरने वाली समानांतर धुरी के बारे में जड़ता का क्षण है"; टी- शरीर का भार; डी- दो समानांतर अक्षों के बीच की दूरी (चित्र 5.9)। जड़त्व आघूर्ण की इकाई है किलोग्राम मीटर वर्ग(किलो-एम2)।

गति
आवेग का क्षण(कोनेदार गति)एक निश्चित अक्ष के चारों ओर घूमने वाले भौतिक बिंदु को घूर्णन अक्ष से उसकी दूरी पर बिंदु के संवेग के उत्पाद के बराबर मान कहा जाता है:
एक निश्चित अक्ष के चारों ओर घूमने वाले पिंड का कोणीय संवेग, पिंड को बनाने वाले बिंदुओं के कोणीय संवेग के योग के बराबर होता है:

चूँकि एक कठोर पिंड के सभी बिंदुओं का कोणीय वेग समान होता है, योग के चिह्न से ω निकालने पर [देखें। (5.29)], हमें मिलता है:
(/ - अक्ष के सापेक्ष शरीर की जड़ता का क्षण), या वेक्टर रूप में:
अतः, कोणीय संवेग एक बिंदु के जड़त्व आघूर्ण और कोणीय वेग के गुणनफल के बराबर होता है। इससे यह निष्कर्ष निकलता है कि कोणीय संवेग और कोणीय वेग सदिशों की दिशाएँ मेल खाती हैं। कोणीय संवेग की इकाई है किलोग्राम-मीटर वर्ग प्रति सेकंड(किलो? एम2? एस -1)।
स्थानांतरीय गति में संवेग के लिए सूत्र (5.31) की तुलना समान सूत्र से करना उपयोगी है।
घूमते हुए पिंड की गतिज ऊर्जा
जब कोई पिंड घूमता है, तो उसकी गतिज ऊर्जा में शरीर के अलग-अलग बिंदुओं की गतिज ऊर्जाएं शामिल होती हैं। ठोस के लिए:
अनुवादात्मक गति के लिए अभिव्यक्ति (5.32) की तुलना समान अभिव्यक्ति से करना उपयोगी है।
विभेदन (5.32), हम घूर्णी गति में गतिज ऊर्जा में एक प्रारंभिक परिवर्तन प्राप्त करते हैं:
घूर्णी गति की गतिशीलता के लिए बुनियादी समीकरण
मान लीजिए कि कठोर पिंड, जिस पर बाहरी बलों द्वारा कार्य किया गया था, पर्याप्त छोटे कोण दा से घूमता है। आइए हम ऐसे घूर्णन के दौरान सभी बाहरी बलों के प्रारंभिक कार्य की बराबरी करें [देखें। (5.13)] गतिज ऊर्जा में प्राथमिक परिवर्तन के लिए [देखें। (5.33)]: एम dα = जेω dω , कहां से:
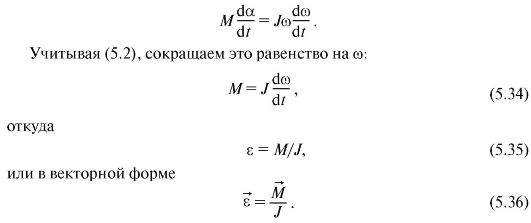
यह वही है बुनियादीघूर्णी गति की गतिशीलता का समीकरण।(5.35) से यह स्पष्ट है कि जड़ता का क्षण घूर्णी गति में किसी पिंड के जड़त्वीय गुणों को दर्शाता है: बाहरी बलों की कार्रवाई के तहत, शरीर का कोणीय त्वरण जितना अधिक होता है, शरीर की जड़ता का क्षण उतना ही छोटा होता है।
घूर्णी गति के लिए मूल समीकरण अनुवादात्मक गति के लिए न्यूटन के दूसरे नियम के समान ही भूमिका निभाता है। इस समीकरण में शामिल भौतिक मात्राएँ क्रमशः बल, द्रव्यमान और त्वरण के अनुरूप हैं।
से (5.34) यह इस प्रकार है:
समय के संबंध में किसी पिंड के कोणीय संवेग का व्युत्पन्न सभी बाह्य बलों के परिणामी आघूर्ण के बराबर होता है।
बल के क्षण और जड़ता के क्षण पर कोणीय त्वरण की निर्भरता को प्रदर्शित किया जा सकता है

चित्र में दिखाए गए डिवाइस की शक्ति के साथ। 5.10. भार के अंतर्गत 1, एक ब्लॉक के ऊपर फेंके गए धागे पर लटका हुआ क्रॉस तेजी से घूमता है। चलता हुआ वजन 2 घूर्णन अक्ष से विभिन्न दूरी पर, आप क्रॉस की जड़ता के क्षण को बदल सकते हैं। भार बदलना, अर्थात्। बल के क्षण और जड़ता के क्षण से, कोई यह सत्यापित कर सकता है कि कोणीय त्वरण बल के क्षण में वृद्धि या जड़ता के क्षण में कमी के साथ बढ़ता है।
5.3. संवेग संरक्षण का नियम
आइए घूर्णी गति के विशेष मामले पर विचार करें, जब बाहरी बलों का कुल क्षण शून्य है। जैसा कि (5.37) से देखा जा सकता है, डीएल/डीटी= 0 पर एम = 0, कहाँ से
इस प्रावधान को कहा जाता है कोणीय संवेग के संरक्षण का नियम: यदि किसी पिंड पर कार्य करने वाले सभी बाह्य बलों का कुल आघूर्ण शून्य है, तो इस पिंड का कोणीय संवेग स्थिर रहता है।
प्रमाण को छोड़ते हुए, हम ध्यान देते हैं कि कोणीय गति के संरक्षण का नियम न केवल बिल्कुल कठोर शरीर के लिए मान्य है।
इस नियम का सबसे दिलचस्प अनुप्रयोग एक सामान्य अक्ष के चारों ओर पिंडों की एक प्रणाली के घूमने से जुड़ा है। इस मामले में, कोणीय गति और कोणीय वेग की वेक्टर प्रकृति को ध्यान में रखना आवश्यक है। तो, एक प्रणाली के लिए जिसमें शामिल है एनएक सामान्य अक्ष के चारों ओर घूमने वाले पिंडों के कोणीय संवेग के संरक्षण के नियम को इस प्रकार लिखा जा सकता है:
आइए इस कानून को दर्शाने वाले कुछ उदाहरण देखें।
प्रारंभिक चरण में कलाबाजी (चित्र 5.11) करने वाला एक जिमनास्ट अपने घुटनों को मोड़ता है और उन्हें अपनी छाती पर दबाता है, जिससे जड़ता का क्षण कम हो जाता है और द्रव्यमान के केंद्र से गुजरने वाली क्षैतिज धुरी के चारों ओर घूमने का कोणीय वेग बढ़ जाता है। छलांग के अंत में, शरीर सीधा हो जाता है, जड़ता का क्षण बढ़ जाता है और कोणीय वेग कम हो जाता है। एक ऊर्ध्वाधर अक्ष के चारों ओर घूर्णन करने वाला एक स्केटर (चित्र 5.12) घूर्णन की शुरुआत में अपने हाथों को शरीर के करीब लाता है, जिससे जड़ता का क्षण कम हो जाता है और कोणीय गति बढ़ जाती है। घूर्णन के अंत में, विपरीत प्रक्रिया होती है: भुजाओं को हिलाने पर जड़ता का क्षण बढ़ जाता है और कोणीय वेग कम हो जाता है, जिससे रुकना आसान हो जाता है।

इसी घटना को ज़ुकोवस्की बेंच पर प्रदर्शित किया जा सकता है, जो एक ऊर्ध्वाधर अक्ष के चारों ओर कम घर्षण के साथ घूमने वाला एक हल्का क्षैतिज मंच है। जब हाथों की स्थिति बदलती है, जड़ता का क्षण और कोणीय वेग बदलता है (चित्र 5.13), कोणीय गति स्थिर रहती है। प्रदर्शन प्रभाव को बढ़ाने के लिए व्यक्ति के हाथों में डम्बल होते हैं। ज़ुकोवस्की बेंच पर आप कोणीय गति के संरक्षण के नियम की वेक्टर प्रकृति का प्रदर्शन कर सकते हैं।
प्रयोगकर्ता, एक स्थिर बेंच पर खड़ा है, एक सहायक से एक ऊर्ध्वाधर अक्ष के चारों ओर घूमने वाला एक साइकिल पहिया प्राप्त करता है (चित्र 5.14, बाएं)। इस मामले में, व्यक्ति और प्लेटफ़ॉर्म-पहिया प्रणाली का कोणीय संवेग केवल पहिये के कोणीय संवेग से निर्धारित होता है:
यहाँ J h व्यक्ति और मंच की जड़ता का क्षण है; जे के और ω κ - जड़ता का क्षण और पहिये की कोणीय गति। चूँकि ऊर्ध्वाधर अक्ष के सापेक्ष बाह्य बलों का क्षण शून्य है एलसंरक्षित है (एल = स्थिरांक).
यदि प्रयोगकर्ता पहिये के घूर्णन अक्ष को 180° घुमाता है (चित्र 5.14, दाएं), तो पहिये का कोणीय संवेग मूल के विपरीत निर्देशित होगा और J K ω K के बराबर होगा। चूँकि पहिए के कोणीय संवेग का वेक्टर बदलता है, और सिस्टम का कोणीय संवेग संरक्षित रहता है, व्यक्ति और प्लेटफ़ॉर्म का कोणीय संवेग अनिवार्य रूप से बदलना होगा; यह अब शून्य 1 के बराबर नहीं होगा। इस मामले में सिस्टम का कोणीय संवेग
1 पहिया अक्ष और प्लेटफार्म रोटेशन अक्ष के बीच थोड़ी सी विसंगति को नजरअंदाज किया जा सकता है।



सूत्र (5.42) का उपयोग करके, प्लेटफ़ॉर्म के साथ-साथ मानव शरीर की जड़ता के क्षण का अनुमान लगाना संभव है, जिसके लिए ω κ, ω 4 को मापना और J k खोजना आवश्यक है। एक समान घूर्णन के कोणीय वेग को मापने की विधि पाठक को ज्ञात है। पहिये के द्रव्यमान को जानने और यह मानते हुए कि द्रव्यमान मुख्य रूप से रिम के साथ वितरित होता है, सूत्र (5.22) का उपयोग करके हम J k निर्धारित कर सकते हैं। त्रुटि को कम करने के लिए, आप साइकिल के पहिये पर विशेष टायर बिछाकर उसके रिम को भारी बना सकते हैं। व्यक्ति को घूर्णन अक्ष के सममित रूप से स्थित होना चाहिए।
प्रदर्शन का एक सरल संस्करण यह माना जाता है कि ज़ुकोवस्की बेंच पर खड़ा एक व्यक्ति स्वयं एक पहिया घुमाता है, जिसे वह एक ऊर्ध्वाधर अक्ष पर रखता है। इस स्थिति में, व्यक्ति और मंच विपरीत दिशाओं में घूमने लगते हैं (चित्र 5.15)।
5.4. घूर्णन की मुक्त अक्षों की अवधारणा
एक निश्चित अक्ष के चारों ओर घूमने वाला शरीर आम तौर पर बीयरिंग या अन्य उपकरणों पर कार्य करता है जो उस अक्ष की स्थिति को स्थिर रखते हैं। उच्च कोणीय वेग और जड़ता के क्षणों पर, ये प्रभाव महत्वपूर्ण हो सकते हैं। हालाँकि, किसी भी पिंड में उन अक्षों का चयन करना संभव है जिनकी दिशा घूर्णन के दौरान बिना किसी विशेष उपकरण के बनाए रखी जाएगी। यह समझने के लिए कि ऐसी कुल्हाड़ियों का चुनाव किस शर्त को पूरा करना चाहिए, निम्नलिखित उदाहरण पर विचार करें।

द्रव्यमान केंद्र के निर्देशांक के साथ (5.43) की तुलना करने पर, हम देखते हैं कि यदि घूर्णन अक्ष द्रव्यमान के केंद्र से होकर गुजरता है तो अक्ष पर कार्य करने वाले बल संतुलित होते हैं।
इस प्रकार, यदि घूर्णन की धुरी द्रव्यमान के केंद्र से होकर छड़ के लंबवत गुजरती है, तो घूर्णन करने वाले पिंड से इस धुरी पर कोई प्रभाव नहीं पड़ेगा। यदि बीयरिंग हटा दिए जाते हैं, तो घूर्णन की धुरी अंतरिक्ष में अपनी स्थिति अपरिवर्तित रखते हुए घूमना शुरू कर देगी, और शरीर इस धुरी के चारों ओर घूमता रहेगा।
घूर्णन कुल्हाड़ियाँ जो विशेष बन्धन के बिना अंतरिक्ष में अपनी दिशा बनाए रखती हैं, मुक्त कहलाती हैं। ऐसी अक्षों के उदाहरण पृथ्वी और शीर्ष के घूर्णन अक्ष, किसी फेंके गए और स्वतंत्र रूप से घूमने वाले पिंड की धुरी आदि हैं।
मनमाने आकार के किसी पिंड में हमेशा द्रव्यमान के केंद्र से गुजरने वाली कम से कम तीन परस्पर लंबवत अक्ष होते हैं, जो घूर्णन के मुक्त अक्ष हो सकते हैं। इन अक्षों को जड़त्व के मुख्य अक्ष कहा जाता है। यद्यपि जड़त्व के सभी तीन मुख्य अक्ष स्वतंत्र हैं, सबसे स्थिर घूर्णन जड़त्व के सबसे बड़े क्षण के साथ अक्ष के चारों ओर होगा। तथ्य यह है कि घर्षण जैसी बाहरी ताकतों की अपरिहार्य कार्रवाई के परिणामस्वरूप, और इस तथ्य के कारण भी कि एक निश्चित अक्ष के चारों ओर घूर्णन को सटीक रूप से सेट करना मुश्किल है, शेष मुक्त अक्षों के चारों ओर घूमना अस्थिर है।
कुछ मामलों में, जब कोई पिंड जड़ता के एक छोटे से क्षण के साथ एक मुक्त अक्ष के चारों ओर घूमता है, तो वह स्वयं इस अक्ष को उच्चतम क्षण के साथ अक्ष में बदल देता है।
इस घटना को निम्नलिखित प्रयोग द्वारा प्रदर्शित किया गया है। एक बेलनाकार छड़ को एक धागे द्वारा विद्युत मोटर से लटकाया जाता है, जो अपने ज्यामितीय अक्ष के चारों ओर घूम सकती है (चित्र 5.17, ए)। इस अक्ष के बारे में जड़ता का क्षण जे 1 = एमआर 2 /2.पर्याप्त उच्च कोणीय वेग पर, छड़ी अपनी स्थिति बदल देगी (चित्र 5.17, बी)। नई धुरी के सापेक्ष जड़ता का क्षण बराबर है जे 2 = एमएल 2/12. यदि l 2 >6R 2, तो J 2 > J 1. नई धुरी के चारों ओर घूर्णन स्थिर होगा।
पाठक अनुभव से स्वतंत्र रूप से सत्यापित कर सकता है कि फेंकी गई माचिस की डिब्बी का घूर्णन बड़े फलक के लंबवत चलने वाली धुरी के सापेक्ष स्थिर है, और अन्य फलक के लंबवत चलने वाली अक्ष के सापेक्ष अस्थिर या कम स्थिर है (चित्र 5.8 देखें)।
मुक्त उड़ान में और विभिन्न छलांगों के दौरान जानवरों और मनुष्यों का घूमना जड़ता के उच्चतम या निम्नतम क्षण के साथ मुक्त अक्षों के आसपास होता है। चूंकि द्रव्यमान के केंद्र की स्थिति शरीर की मुद्रा पर निर्भर करती है, इसलिए विभिन्न मुद्राओं के लिए अलग-अलग मुक्त अक्ष होंगे।

5.5. स्वतंत्रता की डिग्री की अवधारणा
अंतरिक्ष में एक मुक्त सामग्री बिंदु की स्थिति तीन स्वतंत्र निर्देशांक द्वारा निर्दिष्ट की जाती है: x, y, z। यदि बिंदु स्वतंत्र नहीं है, लेकिन चलता है, उदाहरण के लिए, किसी सतह पर, तो सभी तीन निर्देशांक स्वतंत्र नहीं होंगे।

एक यांत्रिक प्रणाली की स्थिति को दर्शाने वाले स्वतंत्र चर को स्वतंत्रता की डिग्री कहा जाता है।
एक मुक्त भौतिक बिंदु में स्वतंत्रता की तीन डिग्री होती है, उदाहरण में - स्वतंत्रता की दो डिग्री। चूँकि एक मोनोआटोमिक गैस के अणु को एक भौतिक बिंदु माना जा सकता है, इसलिए, ऐसे मुक्त अणु में भी स्वतंत्रता की तीन डिग्री होती है।
कुछ और उदाहरण.
दो भौतिक बिंदु 1 और 2 एक दूसरे से मजबूती से जुड़े हुए हैं। दोनों बिंदुओं की स्थिति छह निर्देशांकों द्वारा निर्दिष्ट की जाती है एक्स 1, वाई 1, जेड 1, एक्स 2, वाई 2, जेड 2,जो एक बाधा और एक कनेक्शन के अधीन हैं, गणितीय रूप से एक समीकरण के रूप में व्यक्त किए जाते हैं:
भौतिक रूप से, इसका मतलब है कि भौतिक बिंदुओं के बीच की दूरी हमेशा होती है एलइस मामले में, स्वतंत्रता की डिग्री की संख्या 5 है। माना गया उदाहरण एक डायटोमिक अणु का एक मॉडल है।
तीन भौतिक बिंदु 1, 2 और 3 एक दूसरे से मजबूती से जुड़े हुए हैं। दोस्त। नौ निर्देशांक ऐसी प्रणाली की स्थिति को दर्शाते हैं: एक्स 1 , वाई 1 ,जेड 1, एक्स 2 , वाई 2 , z2, एक्स 3य 3 , ज़ 3 . हालाँकि, बिंदुओं के बीच तीन कनेक्शन केवल छह निर्देशांक की स्वतंत्रता निर्धारित करते हैं। सिस्टम में स्वतंत्रता की छह डिग्री हैं। चूँकि तीन बिंदुओं की स्थिति जो एक ही सीधी रेखा पर नहीं होती है, विशिष्ट रूप से एक कठोर वस्तु की स्थिति निर्धारित करती है, कठोर वस्तु में छह डिग्री की स्वतंत्रता होती है।
यदि इन अणुओं को कठोर संरचनाओं के रूप में माना जाता है, तो त्रिपरमाणुक और बहुपरमाणुक अणुओं की स्वतंत्रता की डिग्री की संख्या समान (छह) होती है।
1 यदि (5.44) से आश्रित निर्देशांक के लिए एक काल्पनिक मान प्राप्त किया जाता है, तो इसका मतलब है कि चयनित स्वतंत्र निर्देशांक किसी दिए गए त्रिज्या के गोले पर स्थित किसी भी बिंदु के अनुरूप नहीं हैं।
वास्तविक बहुपरमाणुक अणुओं में, परमाणु कंपन गति में होते हैं, इसलिए ऐसे अणुओं की स्वतंत्रता की डिग्री की संख्या छह से अधिक होती है।
स्वतंत्रता की डिग्री की संख्या न केवल यांत्रिक प्रणाली की स्थिति को दर्शाने वाले स्वतंत्र चर की संख्या निर्धारित करती है, बल्कि, जो बहुत महत्वपूर्ण है, प्रणाली के स्वतंत्र आंदोलनों की संख्या भी निर्धारित करती है। इस प्रकार, एक मुक्त भौतिक बिंदु की स्वतंत्रता की तीन डिग्री का मतलब है कि बिंदु के किसी भी आंदोलन को तीन समन्वय अक्षों के साथ स्वतंत्र आंदोलनों में विघटित किया जा सकता है। चूँकि किसी बिंदु का कोई आयाम नहीं है, इसलिए उसके घूर्णन के बारे में बात करने का कोई मतलब नहीं है। तो, एक भौतिक बिंदु में अनुवादात्मक गति की स्वतंत्रता की तीन डिग्री होती है। किसी समतल, गोले या अन्य सतह पर एक भौतिक बिंदु में स्थानान्तरणीय गति की दो डिग्री की स्वतंत्रता होती है। एक वक्र के साथ एक भौतिक बिंदु की गति (एक पारंपरिक उदाहरण रेल पर ट्रेन की गति है) अनुवादात्मक गति की एक डिग्री की स्वतंत्रता से मेल खाती है।
एक निश्चित अक्ष के चारों ओर घूमने वाले कठोर पिंड में घूर्णी गति की एक डिग्री की स्वतंत्रता होती है। ट्रेन के पहिये में स्वतंत्रता की दो डिग्री होती हैं: एक घूर्णी गति, और दूसरी ट्रांसलेशनल (पहिया धुरी को रेल के साथ ले जाना)। एक कठोर पिंड की स्वतंत्रता की छह डिग्री का मतलब है कि इस पिंड की किसी भी गति को घटकों में विघटित किया जा सकता है: द्रव्यमान के केंद्र की गति को समन्वय अक्षों के साथ तीन अनुवादात्मक आंदोलनों में विघटित किया जाता है, और घूर्णन में समन्वय अक्षों के बारे में तीन सरल घुमाव होते हैं द्रव्यमान के केंद्र से होकर गुजरना।
चित्र में. 5.18-5.20 स्वतंत्रता की एक, दो और तीन डिग्री के अनुरूप काज जोड़ों को दिखाएं।

चावल। 5.18

चावल। 5.19

चावल। 5.20
5.6. centrifugation
सेंट्रीफ्यूजेशन विषम प्रणालियों को अलग करने (पृथक्करण) की प्रक्रिया है, उदाहरण के लिए, तरल पदार्थों से कण जिसमें वे स्थित हैं, उनके घूर्णन के कारण।
आइए हम गुरुत्वाकर्षण क्षेत्र में अमानवीय प्रणालियों के पृथक्करण पर विचार करें। आइए मान लें कि अलग-अलग घनत्व के कणों का जलीय निलंबन है। समय के साथ, गुरुत्वाकर्षण और उत्प्लावन बल की क्रिया के कारण एफ एकण पृथक्करण होता है: पानी के घनत्व से अधिक घनत्व वाले कण डूब जाते हैं, पानी के घनत्व से कम घनत्व वाले कण तैरते हैं। उदाहरण के लिए, एक सघन व्यक्तिगत कण पर कार्य करने वाला परिणामी बल बराबर होता है:
कहाँ ρ 1 - कण पदार्थ घनत्व; ρ - पानी का घनत्व; वी- कण मात्रा.
यदि ρ 1 और ρ का मान एक दूसरे से थोड़ा भिन्न हो, तो बल एफपीछोटा होता है और पृथक्करण (जमाव) काफी धीरे-धीरे होता है। एक अपकेंद्रित्र (विभाजक) में, अलग किए गए माध्यम को घुमाकर इस तरह का पृथक्करण जबरन किया जाता है।
आइए इस घटना की भौतिकी पर विचार करें।
मान लीजिए कि अपकेंद्रित्र की कार्यशील मात्रा (चित्र 5.21: ए - उपस्थिति; बी - कार्यशील मात्रा का आरेख) पूरी तरह से किसी सजातीय तरल द्वारा व्याप्त है। आइए मानसिक रूप से एक छोटी मात्रा का चयन करें वीकी दूरी पर स्थित इस द्रव का आरघूर्णन अक्ष से OO"। अपकेंद्रित्र के एकसमान घूर्णन के साथ, गुरुत्वाकर्षण और उछाल बल के अलावा, जो एक दूसरे को संतुलित करते हैं, एक सेंट्रिपेटल बल चयनित आयतन पर कार्य करता है। यह आयतन के आसपास के तरल से आने वाला बल है। यह है स्वाभाविक रूप से घूर्णन की धुरी की ओर निर्देशित और इसके बराबर है:
कहाँ ρ द्रव का घनत्व है।
आइए अब मान लें कि आवंटित मात्रा वीएक अलग कण है जिसका पदार्थ घनत्व ρ 1 (ρ 1 Φ ρ) है। आसपास के तरल पदार्थ से कण पर लगने वाला बल नहीं बदलेगा, जैसा कि सूत्र (5.45) से देखा जा सकता है।
किसी कण को तरल के साथ घूमने के लिए, उस पर एक अभिकेन्द्रीय बल का कार्य करना आवश्यक है, जो इसके बराबर है:
कहाँ मी 1कण का द्रव्यमान है, और ρ 1 संगत घनत्व है।

चावल। 5.21
अगर एफ> एफ 1,तब कण घूर्णन अक्ष की ओर गति करता है। अगर एफ< एफ 1,तब द्रव से कण पर प्रभाव उसे वृत्ताकार प्रक्षेपवक्र पर रखने के लिए पर्याप्त नहीं होगा, और कण जड़ता द्वारा परिधि की ओर बढ़ना शुरू कर देगा। पृथक्करण प्रभाव अतिरिक्त बल द्वारा निर्धारित होता है एफ,चयनित कण पर द्रव की ओर से अभिकेंद्री बल F 1 के मान से ऊपर कार्य करना, जो वृत्ताकार गति को निर्धारित करता है:
इस अभिव्यक्ति से पता चलता है कि सेंट्रीफ्यूजेशन का प्रभाव अधिक होता है, अलग किए गए कणों और तरल के घनत्व में अंतर उतना ही अधिक होता है, और यह रोटेशन 1 के कोणीय वेग पर भी महत्वपूर्ण रूप से निर्भर करता है।
आइए सेंट्रीफ्यूजेशन द्वारा पृथक्करण की तुलना गुरुत्वाकर्षण का उपयोग करके पृथक्करण से करें:

1 सूत्र (5.47) निकालते समय गुरुत्वाकर्षण और उत्प्लावन बल को ध्यान में नहीं रखा जाता है, क्योंकि वे घूर्णन की धुरी के साथ निर्देशित होते हैं और सेंट्रीफ्यूजेशन पर मौलिक प्रभाव नहीं डालते हैं।
अल्ट्रासेंट्रीफ्यूज तरल में निलंबित या घुले हुए 100 एनएम से छोटे कणों को अलग करने में सक्षम हैं। उन्होंने बायोपॉलिमर, वायरस और उपकोशिकीय कणों को अलग करने के लिए बायोमेडिकल अनुसंधान में व्यापक आवेदन पाया है।
पृथक्करण की गति जैविक और जैवभौतिकीय अनुसंधान में विशेष रूप से महत्वपूर्ण है, क्योंकि समय के साथ अध्ययन की जा रही वस्तुओं की स्थिति में काफी बदलाव आ सकता है।
मान लीजिए कि बिंदु A पर लगाए गए बल F के प्रभाव में एक निश्चित पिंड, अक्ष OO के चारों ओर घूमने लगता है" (चित्र 1.14)।
बल अक्ष के लंबवत समतल में कार्य करता है। बिंदु O (अक्ष पर स्थित) से बल की दिशा पर डाला गया लंब p कहलाता है ताकत का कंधा. भुजा द्वारा लगाए गए बल का उत्पाद बिंदु O के सापेक्ष बल के क्षण का मापांक निर्धारित करता है:
एम = एफपी=फ्र्सिनα।
शक्ति का क्षण बल के अनुप्रयोग बिंदु और बल वेक्टर के त्रिज्या वेक्टर के वेक्टर उत्पाद द्वारा निर्धारित एक वेक्टर है:
 (3.1) बल आघूर्ण की इकाई न्यूटन मीटर (N·m) है।
(3.1) बल आघूर्ण की इकाई न्यूटन मीटर (N·m) है।
एम की दिशा सही पेंच नियम का उपयोग करके पाई जा सकती है।
आवेग का क्षण कण, कण की त्रिज्या सदिश और उसके संवेग का सदिश गुणनफल है:
 या अदिश रूप में L = rPsinα
या अदिश रूप में L = rPsinα
यह मात्रा सदिश है और सदिश ω के साथ दिशा में मेल खाती है।
§ 3.2 जड़ता का क्षण. स्टीनर का प्रमेय
स्थानांतरीय गति के दौरान पिंडों की जड़ता का माप द्रव्यमान है। घूर्णी गति के दौरान पिंडों की जड़ता न केवल द्रव्यमान पर निर्भर करती है, बल्कि घूर्णन की धुरी के सापेक्ष अंतरिक्ष में इसके वितरण पर भी निर्भर करती है। घूर्णी गति के दौरान जड़त्व की माप को एक मात्रा कहा जाता हैशरीर की जड़ता का क्षण घूर्णन अक्ष के सापेक्ष.
किसी भौतिक बिंदु की जड़ता का क्षणघूर्णन अक्ष के सापेक्ष इस बिंदु के द्रव्यमान और अक्ष से इसकी दूरी के वर्ग के गुणनफल को कहा जाता है:
मैं मैं =एम मैं आर मैं 2 (3.2)
घूर्णन अक्ष के सापेक्ष पिंड की जड़ता का क्षणइस शरीर को बनाने वाले भौतिक बिंदुओं की जड़ता के क्षणों का योग ज्ञात करें:
 (3.3)
(3.3)
सामान्य स्थिति में, यदि शरीर ठोस है और छोटे द्रव्यमान dm वाले बिंदुओं के संग्रह का प्रतिनिधित्व करता है, तो जड़ता का क्षण एकीकरण द्वारा निर्धारित किया जाता है:
 (3.4)
(3.4)
यदि शरीर सजातीय है और उसका घनत्व है  , फिर शरीर की जड़ता का क्षण
, फिर शरीर की जड़ता का क्षण
 (3.5)
(3.5)
किसी पिंड की जड़ता का क्षण इस बात पर निर्भर करता है कि वह किस अक्ष पर घूमता है और पिंड का द्रव्यमान पूरे आयतन में कैसे वितरित होता है।
नियमित ज्यामितीय आकार और आयतन पर द्रव्यमान का एक समान वितरण वाले पिंडों की जड़ता का क्षण सबसे आसानी से निर्धारित किया जाता है।
एक सजातीय छड़ की जड़ता का क्षणजड़ता के केंद्र से गुजरने वाली और छड़ के लंबवत अक्ष के सापेक्ष
 (3.6)
(3.6)
एक सजातीय सिलेंडर की जड़ता का क्षणइसके आधार पर लंबवत और जड़ता के केंद्र से गुजरने वाली धुरी के सापेक्ष,
 (3.7)
(3.7)
पतली दीवार वाले सिलेंडर की जड़ता का क्षणया इसके आधार के तल के लंबवत और इसके केंद्र से गुजरने वाली धुरी के सापेक्ष घेरा,
 (3.8)
(3.8)
निष्क्रियता के पल व्यास के सापेक्ष गेंद
 (3.9)
(3.9)
आइए एक उदाहरण देखें . आइए हम जड़ता के केंद्र से गुजरने वाली धुरी और घूर्णन के विमान के लंबवत के सापेक्ष डिस्क की जड़ता का क्षण निर्धारित करें। डिस्क द्रव्यमान - मी, त्रिज्या - आर।
रिंग का क्षेत्रफल (चित्र 3.2) के बीच घिरा हुआ है
r और r + dr, dS = 2πr·dr के बराबर है। डिस्क क्षेत्र S = πR 2.
इस तरह,  . तब
. तब
 या
या 
के अनुसार
पिंडों की जड़ता के क्षणों के लिए दिए गए सूत्र इस शर्त के तहत दिए गए हैं कि घूर्णन की धुरी जड़ता के केंद्र से होकर गुजरती है। किसी मनमाने अक्ष के सापेक्ष किसी पिंड की जड़ता के क्षण निर्धारित करने के लिए, आपको इसका उपयोग करना चाहिए स्टीनर का प्रमेय : घूर्णन के एक मनमाने अक्ष के सापेक्ष किसी पिंड की जड़ता का क्षण दिए गए अक्ष के समानांतर और पिंड के द्रव्यमान के केंद्र से गुजरने वाली धुरी के सापेक्ष शरीर की जड़ता के क्षण के योग के बराबर होता है, और अक्षों के बीच की दूरी के वर्ग द्वारा शरीर के द्रव्यमान का गुणनफल:
 (3.11)
(3.11)
जड़त्व आघूर्ण की इकाई किलोग्राम मीटर वर्ग (किलो मीटर 2) है।
इस प्रकार, स्टीनर के प्रमेय के अनुसार, इसके अंत से गुजरने वाली धुरी के सापेक्ष एक सजातीय छड़ की जड़ता का क्षण बराबर है
 (3.12)
(3.12)
सभी प्रकार की घूर्णी गति में से, हम केवल एक निश्चित अक्ष के चारों ओर किसी पिंड के घूमने पर विचार करेंगे।
शक्ति का क्षण
शक्ति का क्षण,जब कोई बल किसी ठोस पिंड पर कार्य करता है तो उसके घूर्णी प्रभाव को दर्शाने वाली मात्रा; यांत्रिकी की बुनियादी अवधारणाओं में से एक है। अंतर करना शक्ति का क्षणकेंद्र के सापेक्ष (ध्रुव बिंदु) और अक्ष के सापेक्ष।
बल का क्षण (समानार्थी शब्द: टोक़, टोक़, टोक़, टोक़) निश्चित बिंदु 0 के सापेक्ष(डंडे) सदिश राशि कहलाती है वेक्टर उत्पाद त्रिज्या के बराबर– वेक्टर एक बिंदु से खींचा गया 0 (डंडे) बल अनुप्रयोग के बिंदु A को, बल सदिश को : ![]() .
.
बल के क्षण की दिशा बाएं हाथ के नियम से भी निर्धारित की जा सकती है: बाएं हाथ की चार अंगुलियों को पहले कारक की दिशा में रखें, दूसरा कारक हथेली में प्रवेश करता है, समकोण पर मुड़ा हुआ अंगूठा इंगित करेगा बल के क्षण की दिशा. बल के क्षण का सदिश हमेशा उस तल के लंबवत होता है जिसमें सदिश और स्थित होते हैं।
 चावल। 68. चावल। 68. |
शक्ति का एक क्षण एक निश्चित अक्ष के सापेक्ष बल के क्षण के वेक्टर के इस अक्ष पर प्रक्षेपण के बराबर एक अदिश राशि कहलाती है , एक मनमाना बिंदु के सापेक्ष परिभाषित दी गई धुरी(चित्र 68)। शक्ति का क्षणअक्ष के सापेक्ष, मात्रा बीजगणितीय है .
बल के क्षण की अवधारणा का उपयोग करके, हम एक अक्ष पर स्थिर किसी पिंड के संतुलन की स्थितियों को नए तरीके से तैयार कर सकते हैं। इस स्थिति को कहा जाता है आघूर्णों का नियम: यदि किसी अक्ष पर स्थिर पिंड पर कई बल कार्य करते हैं, तो अक्ष पर स्थिर पिंड के संतुलन में रहने के लिए, पिंड पर कार्य करने वाले सभी बलों के आघूर्णों का बीजगणितीय योग शून्य के बराबर होना चाहिए:
 चावल। 69. चावल। 69. |
उदाहरण:
1). पाना
 चावल। 70. चावल। 70. |
2). मान लीजिए कि घूर्णन अक्ष के लंबवत तल में किसी पिंड पर एक बल कार्य करता है। आइए हम इस बल को दो घटकों में विघटित करें: और (चित्र 70)।
बल घूर्णन अक्ष को पार करता है और इसलिए पिंड के घूर्णन को प्रभावित नहीं करता है। घटक के प्रभाव में, शरीर धुरी के चारों ओर एक घूर्णी गति करेगा। घूर्णन अक्ष से उस रेखा तक की दूरी जिसके अनुदिश बल कार्य करता है, बल की भुजा कहलाती है। बिंदु 0 के सापेक्ष बल का क्षण बल मापांक और भुजा का गुणनफल है:।
उस बल के क्षण को ध्यान में रखते हुए ![]() वेक्टर बीजगणित के दृष्टिकोण से, यह अभिव्यक्ति बल और इस बल के अनुप्रयोग के बिंदु पर खींची गई त्रिज्या वेक्टर के वेक्टर उत्पाद का प्रतिनिधित्व करती है।
वेक्टर बीजगणित के दृष्टिकोण से, यह अभिव्यक्ति बल और इस बल के अनुप्रयोग के बिंदु पर खींची गई त्रिज्या वेक्टर के वेक्टर उत्पाद का प्रतिनिधित्व करती है।
इस प्रकार, बिंदु 0 के सापेक्ष बल का क्षण एक सदिश राशि है और इसके बराबर है:
बल के क्षण का वेक्टर वेक्टर और के माध्यम से खींचे गए विमान के लंबवत निर्देशित होता है, और उनके साथ वैक्टर का एक दाहिना हाथ ट्रिपल बनाता है (जब वेक्टर के शीर्ष से देखा जाता है, तो यह स्पष्ट है कि सबसे कम दूरी के साथ घूर्णन k से वामावर्त दिशा में होता है)।
उदाहरण:
1). लीवर
लीवर एक कठोर पिंड है जिसमें घूर्णन की एक निश्चित धुरी होती है और यह उन बलों के अधीन होता है जो इसे इस धुरी के चारों ओर घुमाते हैं।
लीवर के उदाहरण रिंच, विभिन्न पैडल, नटक्रैकर, दरवाजे आदि हैं।
आघूर्ण के नियम के अनुसार कोई लीवर (किसी भी प्रकार का) तभी संतुलित होता है . चूँकि और, हमें मिलता है। अंतिम सूत्र से यह निष्कर्ष निकलता है कि:
अर्थात।, जब एक लीवर दो बलों की कार्रवाई के तहत संतुलन में होता है, तो इन बलों के मॉड्यूल उनकी भुजाओं के व्युत्क्रमानुपाती होते हैं।वे। लीवर की सहायता से, लीवरेज अनुपात जितना अधिक होगा, ताकत में लाभ उतना ही अधिक होगा। व्यवहार में इसका व्यापक रूप से उपयोग किया जाता है।
2). बलों की जोड़ी
 चावल। 71. चावल। 71. |
किसी पिंड पर अलग-अलग बिंदुओं पर लगाए गए समान परिमाण के दो प्रतिसमानांतर बलों को बलों की एक जोड़ी कहा जाता है। बलों की एक जोड़ी के उदाहरण वे बल हैं जो कार के स्टीयरिंग व्हील पर लगाए जाते हैं (चित्र 71)। ए), द्विध्रुव पर कार्यरत विद्युत बल (चित्र 71)। बी), चुंबकीय सुई पर कार्यरत चुंबकीय बल (चित्र 71)। वी) वगैरह।
बलों की एक जोड़ी का कोई परिणाम नहीं होता है, अर्थात, इन बलों की संयुक्त कार्रवाई को एक बल की कार्रवाई से प्रतिस्थापित नहीं किया जा सकता है। इसलिए, बलों की एक जोड़ी किसी पिंड की स्थानांतरीय गति का कारण नहीं बन सकती, बल्कि केवल उसे घूमने का कारण बनती है।
यदि, जब कोई पिंड बलों की एक जोड़ी के प्रभाव में घूमता है, तो इन बलों की दिशाएँ नहीं बदलती हैं (चित्र 71) बी, सी), तब पिंड का घूर्णन तब तक होता है जब तक दोनों बल पिंड के घूर्णन अक्ष से गुजरने वाली एक सीधी रेखा के साथ एक दूसरे के विपरीत कार्य नहीं करते हैं।
मान लीजिए कि बलों की एक जोड़ी एक ऐसे पिंड पर कार्य करती है जिसका घूर्णन अक्ष O निश्चित है। इन बलों के क्षण और (चित्र 72)। क्षणों का योग ![]() , इसलिए, शरीर संतुलन में नहीं है।
, इसलिए, शरीर संतुलन में नहीं है।
 चावल। 72. चावल। 72. |
यदि बलों की एक जोड़ी किसी ऐसे पिंड पर कार्य करती है जिसके घूर्णन की कोई निश्चित धुरी नहीं है, तो यह इस पिंड के द्रव्यमान के केंद्र से गुजरने वाली धुरी के चारों ओर इस पिंड के घूमने का कारण बनता है।
गति
कोणीय गति (गतिज गति, कोणीय गति, कक्षीय गति, कोणीय गति)घूर्णी गति की मात्रा को दर्शाता है। एक मात्रा जो इस बात पर निर्भर करती है कि कितना द्रव्यमान घूम रहा है, इसे घूर्णन की धुरी के सापेक्ष कैसे वितरित किया जाता है, और घूर्णन किस गति से होता है।
यह ध्यान दिया जाना चाहिए कि यहाँ घूर्णन को व्यापक अर्थ में समझा जाता है, न कि केवल एक अक्ष के चारों ओर नियमित घूर्णन के रूप में। उदाहरण के लिए, जब कोई पिंड किसी मनमाने काल्पनिक बिंदु से आगे एक सीधी रेखा में चलता है जो गति की रेखा पर नहीं है, तो उसमें भी कोणीय गति होती है। संभवतः वास्तविक घूर्णी गति का वर्णन करने में कोणीय गति द्वारा सबसे बड़ी भूमिका निभाई जाती है। हालाँकि, यह समस्याओं के एक व्यापक वर्ग के लिए बेहद महत्वपूर्ण है (विशेषकर यदि समस्या में केंद्रीय या अक्षीय समरूपता है, लेकिन केवल इन मामलों में नहीं)।
 चावल। 73. चावल। 73. |
गति किसी मूल के सापेक्ष भौतिक बिंदु(इसलिए - पोल) इसकी त्रिज्या वेक्टर के वेक्टर उत्पाद द्वारा निर्धारित किया जाता है और गति(चित्र 73):
![]() ,
,
चयनित संदर्भ बिंदु के सापेक्ष कण का त्रिज्या वेक्टर कहां है जो किसी दिए गए संदर्भ फ्रेम में स्थिर है, और कण की गति है।
कोणीय गति का मापांक बराबर है: ![]() , कहा पे - नाड़ी भुजा, बिंदु 0 - ध्रुव, बिंदु –
आवेग वेक्टर के अनुप्रयोग का बिंदु.
, कहा पे - नाड़ी भुजा, बिंदु 0 - ध्रुव, बिंदु –
आवेग वेक्टर के अनुप्रयोग का बिंदु.
चूंकि कोणीय गति वेक्टर उत्पाद द्वारा निर्धारित की जाती है, यह वेक्टर और दोनों के लिए लंबवत एक छद्मवेक्टर है। हालाँकि, एक स्थिर अक्ष के चारों ओर घूमने के मामलों में, कोणीय गति को छद्मवेक्टर के रूप में नहीं, बल्कि एक अदिश के रूप में रोटेशन की धुरी पर इसके प्रक्षेपण पर विचार करना सुविधाजनक है, जिसका संकेत रोटेशन की दिशा पर निर्भर करता है।
यदि मूल बिंदु से गुजरने वाली ऐसी धुरी का चयन किया जाता है, तो उस पर कोणीय गति के प्रक्षेपण की गणना करने के लिए, दो वैक्टरों के वेक्टर उत्पाद को खोजने के लिए सामान्य नियमों के अनुसार कई तकनीकों को निर्दिष्ट किया जा सकता है:
![]() ,
,
 चावल। 74. चावल। 74. |
और के बीच का कोण कहां है, यह निर्धारित किया जाता है ताकि घूर्णन अक्ष के सकारात्मक भाग पर स्थित एक पर्यवेक्षक के दृष्टिकोण से घूर्णन वामावर्त हो (चित्र 74)। गणना में घूर्णन की दिशा महत्वपूर्ण है, क्योंकि यह वांछित प्रक्षेपण का संकेत निर्धारित करती है।
कोणीय संवेग की परिभाषा से यह निष्कर्ष निकलता है कि यह योगात्मक है। कई कणों के लिए, कोणीय गति को निम्नलिखित शब्दों के (वेक्टर) योग के रूप में परिभाषित किया गया है: , सिस्टम में शामिल प्रत्येक कण का त्रिज्या वेक्टर और संवेग कहां और कहां है, जिसका कोणीय संवेग निर्धारित होता है। एक कठोर शरीर के मामले में, समस्या एकीकरण में कम हो जाती है: .
उदाहरण:
त्रिज्या के एक वृत्त में घूमते हुए द्रव्यमान के एक भौतिक बिंदु की गति का संवेग (चित्र 75): .
प्रकृति का सबसे महत्वपूर्ण नियम है कोणीय गति के संरक्षण का नियम :एक जड़त्वीय संदर्भ फ्रेम में, कणों की एक बंद प्रणाली का कोणीय संवेग स्थिर रहता है: .
जैसा कि आधुनिक भौतिकी (ई. नोएदर प्रमेय) में सिद्ध है, कोणीय गति के संरक्षण का नियम एक परिणाम है अंतरिक्ष की आइसोट्रॉपी.
निष्क्रियता के पल
यह ज्ञात है कि जब कोई ठोस पिंड घूमता है, तो वह एक निश्चित स्थिरता (एक लुढ़कता हुआ सिक्का, एक घेरा) प्राप्त कर लेता है।
न्यूटन के प्रथम नियम के अनुरूप, हम कह सकते हैं:
द्रव्यमान के केंद्र से गुजरने वाली कुछ अक्षों के चारों ओर घूमने वाला एक कठोर शरीर बाहरी बलों की कार्रवाई का अनुभव नहीं करता है और अनिश्चित काल तक घूर्णन बनाए रखता है।
 चावल। 76. चावल। 76. |
मान लीजिए कि द्रव्यमान का भौतिक बिंदु बल के प्रभाव में त्रिज्या के एक वृत्त के अनुदिश घूमता है (चित्र 76)।
फिर, न्यूटन के दूसरे नियम के अनुसार: , , बिंदु का कोणीय त्वरण कहाँ है; यह यहाँ से निम्नानुसार है: , रोटेशन की धुरी के सापेक्ष बल का क्षण कहां है।
आइए निरूपित करें: ![]() – घूर्णन बिंदु की जड़ता का क्षण.
– घूर्णन बिंदु की जड़ता का क्षण.
फिर बिंदु पर कार्य करने वाले बल का क्षण:।
घूर्णन अक्ष के सापेक्ष किसी पिंड की जड़ता का क्षण उसके सभी बिंदुओं की जड़ता के क्षणों के योग के बराबर होता है: ![]() . गणितीय रूप से, समस्या एकीकरण पर आती है।
. गणितीय रूप से, समस्या एकीकरण पर आती है।
जड़ता का क्षणI–एक अदिश राशि जो किसी पिंड में द्रव्यमान के वितरण को दर्शाती है और द्रव्यमान के साथ-साथ घूर्णी गति में पिंड की जड़ता का माप है.
एक ही पिंड में अलग-अलग अक्षों के बारे में जड़ता के अलग-अलग क्षण हो सकते हैं।
पिंड के सापेक्ष अक्ष की दी गई दिशा के लिए, इस अक्ष के सापेक्ष पिंड की जड़ता का क्षण सबसे छोटा होगा, यदि अक्ष पिंड के द्रव्यमान के केंद्र से होकर गुजरता है(टी। साथ), अर्थात। .
पिंड के द्रव्यमान केंद्र से गुजरने वाली अक्षों में तीन विशेष परस्पर लंबवत अक्ष होते हैं। इन अक्षों के चारों ओर समान रूप से घूमने पर, शरीर का बीयरिंगों पर कोई प्रभाव नहीं पड़ता है। इन अक्षों को कहा जाता है मुख्य अक्ष. मनमाने शरीर के आकार के साथ, उन्हें ढूंढना मुश्किल है। लेकिन सममित निकायों के लिए मुख्य अक्षों की स्थिति आसानी से निर्धारित की जाती है। मुख्य अक्षों के सापेक्ष किसी पिंड की जड़ता के क्षण कहलाते हैं जड़ता के मुख्य क्षण.
सरल आकार के पिंडों की जड़ता के मुख्य क्षण
| घूर्णन के कुछ अक्षों के सापेक्ष सरलतम रूप के सजातीय पिंडों की जड़ता के क्षण | |||
| शरीर | विवरण | अक्ष स्थिति ए | निष्क्रियता के पल |
| | सामग्री बिंदु द्रव्यमान एम | दूरी पर आरएक बिंदु से, स्थिर | |
 | खोखली पतली दीवार वाला सिलेंडर या त्रिज्या वलय आरऔर जनता एम | सिलेंडर अक्ष | |
 | ठोस सिलेंडर या त्रिज्या डिस्क आरऔर जनता एम | सिलेंडर अक्ष | |
 | खोखला मोटी दीवार वाला द्रव्यमान सिलेंडर एमबाहरी त्रिज्या के साथ र 2और आंतरिक त्रिज्या आर 1(पाइप) | सिलेंडर अक्ष | |
 | एलऔर जनता एम | धुरी छड़ के लंबवत है और उसके द्रव्यमान केंद्र से होकर गुजरती है | |
 | सीधी पतली लंबाई वाली छड़ एलऔर जनता एम | धुरी छड़ के लंबवत है और उसके सिरे से होकर गुजरती है | |
 | पतली दीवार वाला त्रिज्या क्षेत्र आरऔर जनता एम | धुरी गोले के केंद्र से होकर गुजरती है | |
 | त्रिज्या गेंद आरऔर जनता एम | धुरी गेंद के केंद्र से होकर गुजरती है |
स्टीनर का प्रमेय
एक मनमाना अक्ष के सापेक्ष किसी पिंड की जड़ता का क्षण स्टीनर के प्रमेय द्वारा निर्धारित किया जाता है:
 चावल। 77. चावल। 77. |
शरीर की जड़ता का क्षण एक मनमाना अक्ष के सापेक्ष जड़ता के क्षण के योग के बराबर है अक्ष के सापेक्ष,दिए गए के समानांतर और शरीर के जड़त्व केंद्र से होकर गुजर रहा है, शरीर के द्रव्यमान का गुणनफल, अक्षों के बीच की दूरी के वर्ग का गुणनफल(चित्र 77)।
जहां एक मनमाना अक्ष है, वहां अक्षों के बीच की दूरी है।
स्टीनर के प्रमेय का गणितीय सूत्रीकरण: ![]() , शरीर का द्रव्यमान कहाँ है।
, शरीर का द्रव्यमान कहाँ है।
उदाहरण।
इसके सिरे से गुजरने वाली धुरी के सापेक्ष छड़ की जड़ता का क्षण बराबर है:
छड़ के द्रव्यमान केंद्र से गुजरने वाली धुरी के सापेक्ष छड़ का जड़त्व आघूर्ण कहाँ है?
एक निश्चित अक्ष के सापेक्ष एक कठोर पिंड की घूर्णी गति की गतिशीलता के लिए समीकरण
पिछले पैराग्राफ से ( निष्क्रियता के पल) इससे यह निष्कर्ष निकलता है कि वृत्त में घूमने वाले उस भौतिक बिंदु के लिए निम्नलिखित संबंध सत्य है: .
भौतिक बिंदुओं से युक्त एक ठोस निकाय के लिए: ![]() ; ,हम पाते हैं: ।
; ,हम पाते हैं: ।
समीकरण (1) एक घूमते हुए कठोर पिंड की गतिशीलता का समीकरण है (घूर्णी गति की गतिशीलता का मूल समीकरण):
किसी कठोर पिंड का कोणीय त्वरण, एक निश्चित अक्ष के चारों ओर घूमना, सभी बाहरी ताकतों के कुल क्षण के सीधे आनुपातिक, शरीर पर क्रिया करना, और इसकी जड़ता के क्षण के व्युत्क्रमानुपाती होता है।
आइए समीकरण (1) को इस प्रकार प्रस्तुत करें:
इस तथ्य को ध्यान में रखते हुए  , शरीर का कोणीय संवेग कहां है। तब: । (2)
, शरीर का कोणीय संवेग कहां है। तब: । (2)
समीकरण (2) एक घूमते हुए कठोर पिंड की गतिशीलता का समीकरण भी है (घूर्णी गति की गतिशीलता का मूल समीकरण):
एक निश्चित अक्ष के सापेक्ष किसी पिंड के कोणीय संवेग में परिवर्तन की दर सभी बाह्य बलों के समान अक्ष के सापेक्ष परिणामी क्षण के बराबर होती है, शरीर से जुड़ा हुआ.
समीकरण (1) और (2) से यह निम्नानुसार है:  .
.
तब हमें मिलता है: . (3)
 चावल। 78. चावल। 78. |
यदि कणों की प्रणाली बंद है, तो बाहरी बल उस पर कार्य नहीं करते हैं, तो बाहरी बलों का क्षण, अर्थात। संवेग संरक्षण का नियम प्राप्त होता है। समीकरण (3) को ध्यान में रखते हुए हम प्राप्त करते हैं:
इसी तरह की संपत्ति का उपयोग तब किया जाता है जब फिगर स्केटर्स बर्फ पर दावतें करते हैं, कलाबाज़ों द्वारा कलाबाज़ी करते हैं।
घूमते हुए कठोर पिंड की गतिज ऊर्जा
घूमते हुए कठोर पिंड में ऊर्जा होती है।
जब एक कठोर पिंड एक निश्चित अक्ष के सापेक्ष घूमता है, तो इसके व्यक्तिगत द्रव्यमान तत्व विभिन्न त्रिज्याओं के वृत्तों का वर्णन करते हैं और अलग-अलग रैखिक वेग रखते हैं। हालाँकि, शरीर के सभी बिंदुओं के घूर्णन का कोणीय वेग समान है:
 .
.
किसी पिंड की गतिज ऊर्जा उसके सभी पिंडों की गतिज ऊर्जाओं का योग है:
 ।क्योंकि , तो हमें मिलता है:
।क्योंकि , तो हमें मिलता है:
आइए हम इस बात को ध्यान में रखें कि किसी पिंड की जड़ता का क्षण उसके सभी बिंदुओं की जड़ता के क्षणों के योग के बराबर है: ![]() .
.
अंतिम संबंध को ध्यान में रखते हुए, हम एक घूमते हुए कठोर पिंड की गतिज ऊर्जा के लिए अंतिम अभिव्यक्ति प्राप्त करते हैं:
किसी कठोर पिंड की समतल गति के मामले में, इसकी कुल गतिज ऊर्जा बराबर होती है:
 .
.
अनुवादात्मक और घूर्णी गति के बीच सादृश्य
एक निश्चित अक्ष के चारों ओर एक कठोर पिंड की गति और एक व्यक्तिगत भौतिक बिंदु की गति (या किसी पिंड की अनुवादात्मक गति) के बीच एक करीबी और दूरगामी सादृश्य है। एक बिंदु की गतिकी से प्रत्येक रैखिक मात्रा एक कठोर पिंड के घूर्णन की गतिकी से समान मात्रा से मेल खाती है। निर्देशांक कोण, रैखिक गति से मेल खाता है , कोणीय वेग, रैखिक (स्पर्शरेखा) त्वरण - कोणीय त्वरण।
| आगे बढ़ना | घूर्णी गति | ||||
| गति की गतिज विशेषताएँ | |||||
| पथ | एस | एम | घूर्णन का कोण | जे | खुश |
| समय | टी | साथ | अवधि | टी | साथ |
| रफ़्तार | एमएस | कोणीय वेग | डब्ल्यू | रेड/एस | |
| त्वरण | ए | एम/एस 2 | कोणीय त्वरण | इ | रेड/एस 2 |
| गतिशील ड्राइविंग विशेषताएँ | |||||
| वज़न | एम | किलोग्राम | निष्क्रियता के पल | जे | किलोग्राम × मी 2 |
| बल | एफ | एन | शक्ति का क्षण | एम | एन × एम |
| नाड़ी | पी | किग्रा×मीटर/से | गति | एल=जे×डब्ल्यू | किलोग्राम × एम 2/एस |
| न्यूटन का दूसरा नियम | एफ=मा; एफ=डीपी/डीटी | घूर्णी गति की गतिशीलता का समीकरण | एम=जे×ई; एम=डीएल/डीटी | ||
| काम | dA=F×dS | जे | काम | dA=M×dj | जे |
| गतिज ऊर्जा | ई के =(एम 2)/2 | जे | गतिज ऊर्जा | ई के बीपी =(जेडब्ल्यू 2)/2 | जे |
| शक्ति | एन=एफ | डब्ल्यू | शक्ति | एन=एम×डब्ल्यू | डब्ल्यू |
अनुवादात्मक गति को घूर्णी माना जा सकता है, जिसमें घूर्णन की त्रिज्या अनंत की ओर और कोणीय वेग शून्य की ओर प्रवृत्त होता है।
 चावल। 79. चावल। 79. |
5. सापेक्षता का यांत्रिक (शास्त्रीय) सिद्धांत
(गैलीलियो का सापेक्षता का सिद्धांत)
जी गैलीलियो की संक्षिप्त जीवनी
गैलीलियो गैलीलियो(15.II.1564 - 8.I.1642) - एक उत्कृष्ट इतालवी भौतिक विज्ञानी और खगोलशास्त्री, सटीक प्राकृतिक विज्ञान के संस्थापकों में से एक, अकादमी डी लिंस (1611) के सदस्य, पीसा में पैदा हुए। 1581 में उन्होंने पीसा विश्वविद्यालय में प्रवेश लिया, जहाँ उन्होंने चिकित्सा का अध्ययन किया। लेकिन, ज्यामिति और यांत्रिकी, विशेष रूप से आर्किमिडीज़ और यूक्लिड के कार्यों से आकर्षित होकर, उन्होंने अपने शैक्षिक व्याख्यानों के साथ विश्वविद्यालय छोड़ दिया और फ्लोरेंस लौट आए, जहां उन्होंने चार वर्षों तक अकेले गणित का अध्ययन किया।
1589 से - पीसा विश्वविद्यालय में प्रोफेसर, 1592-1610 में - पडुआ विश्वविद्यालय में, बाद में - ड्यूक कोसिमो द्वितीय डी' मेडिसी के दरबारी दार्शनिक।
वैज्ञानिक सोच के विकास पर उनका महत्वपूर्ण प्रभाव था। उन्हीं से एक विज्ञान के रूप में भौतिकी की उत्पत्ति हुई। मानवता गैलीलियो के यांत्रिकी के दो सिद्धांतों का ऋणी है, जिन्होंने न केवल यांत्रिकी, बल्कि संपूर्ण भौतिकी के विकास में एक बड़ी भूमिका निभाई। यह सीधी और एकसमान गति के लिए सापेक्षता का प्रसिद्ध गैलीलियन सिद्धांत और गुरुत्वाकर्षण के त्वरण की स्थिरता का सिद्धांत है।
गैलीलियो ने जड़त्व का नियम (1609), मुक्त गिरावट के नियम, एक झुके हुए तल पर किसी पिंड की गति (1604 - 09) और क्षितिज पर एक कोण पर फेंके गए पिंड की स्थापना की, गतियों के योग के नियम की खोज की और पेंडुलम के दोलन की अवधि की स्थिरता का नियम (दोलन के समकालिकता की घटना, 1583)। गतिशीलता की उत्पत्ति गैलीलियो से हुई है।
जुलाई 1609 में, गैलीलियो ने अपना पहला टेलीस्कोप बनाया - एक उत्तल और अवतल लेंस से युक्त एक ऑप्टिकल प्रणाली - और व्यवस्थित खगोलीय अवलोकन शुरू किया। यह दूरबीन का पुनर्जन्म था, जो लगभग 20 वर्षों की अस्पष्टता के बाद वैज्ञानिक ज्ञान का एक शक्तिशाली उपकरण बन गया। अत: गैलीलियो को प्रथम दूरबीन का आविष्कारक माना जा सकता है। उन्होंने तुरंत अपनी दूरबीन में सुधार किया और, जैसा कि उन्होंने समय के साथ लिखा, "अपने लिए एक ऐसा अद्भुत उपकरण बनाया कि इसकी मदद से वस्तुएं लगभग एक हजार गुना बड़ी और साधारण आंख से देखने पर तीस गुना से भी ज्यादा करीब दिखाई देती थीं।" 12 मार्च, 1610 को वेनिस में प्रकाशित ग्रंथ "द स्टाररी मैसेंजर" में, उन्होंने दूरबीन की मदद से की गई खोजों का वर्णन किया: चंद्रमा पर पहाड़ों की खोज, बृहस्पति के चार उपग्रह, इस बात का प्रमाण है कि आकाशगंगा में शामिल हैं कई सितारे.
गैलीलियो की खगोलीय खोजों ने वैज्ञानिक विश्वदृष्टि के विकास में एक बड़ी भूमिका निभाई; वे कोपरनिकस की शिक्षाओं की शुद्धता, अरस्तू और टॉलेमी की प्रणाली की भ्रांति के बारे में स्पष्ट रूप से आश्वस्त थे, और हेलियोसेंट्रिक प्रणाली की जीत और स्थापना में योगदान दिया। दुनिया। 1632 में, प्रसिद्ध "विश्व की दो प्रमुख प्रणालियों पर संवाद" प्रकाशित हुआ, जिसमें गैलीलियो ने कोपरनिकस की सूर्य केन्द्रित प्रणाली का बचाव किया। पुस्तक के प्रकाशन ने पादरी को क्रोधित कर दिया, इनक्विजिशन ने गैलीलियो पर विधर्म का आरोप लगाया और एक परीक्षण आयोजित करके, उन्हें कोपर्निकन शिक्षाओं को सार्वजनिक रूप से त्यागने के लिए मजबूर किया, और संवाद पर प्रतिबंध लगा दिया। 1633 में मुकदमे के बाद, गैलीलियो को "पवित्र धर्माधिकरण का कैदी" घोषित किया गया और उन्हें पहले रोम में और फिर फ्लोरेंस के पास आर्कर्ट्री में रहने के लिए मजबूर किया गया। हालाँकि, गैलीलियो ने अपनी वैज्ञानिक गतिविधि नहीं रोकी; अपनी बीमारी से पहले (1637 में, गैलीलियो ने अंततः अपनी दृष्टि खो दी), उन्होंने "विज्ञान की दो नई शाखाओं के संबंध में वार्तालाप और गणितीय प्रमाण" काम पूरा किया, जिसमें उनके भौतिक अनुसंधान का सार था।
उन्होंने थर्मोस्कोप का आविष्कार किया, जो थर्मामीटर का प्रोटोटाइप है, ठोस पदार्थों के विशिष्ट गुरुत्व को निर्धारित करने के लिए हाइड्रोस्टैटिक संतुलन को डिजाइन किया (1586), और हवा के विशिष्ट गुरुत्व को निर्धारित किया। उन्होंने घड़ी में पेंडुलम का उपयोग करने का विचार सामने रखा। भौतिक अनुसंधान हाइड्रोस्टैटिक्स, सामग्रियों की ताकत आदि के लिए भी समर्पित है।
निबंध:
1. विश्व की दो सबसे महत्वपूर्ण प्रणालियों, टॉलेमिक और कोपर्निकन के बारे में संवाद। एम.-एल. ओजीआईज़, 1948।
2. परख मास्टर / अनुवाद। यू. ए. डेनिलोवा। - एम.: नौका, 1987. - 272 पी. - (श्रृंखला "प्राकृतिक विज्ञान के क्लासिक्स के लोकप्रिय कार्य")।
3. विज्ञान की दो नई शाखाओं से संबंधित वार्तालाप और गणितीय प्रमाण (कार्य खंड 1)। जीटीटीआई. एम-एल. 1934.
4. पानी में तैरते पिंडों और उसमें घूमने वाले पिंडों के बारे में तर्क। सीटी में: आर्किमिडीज़। स्टैविन. गैलीलियो. पास्कल। जाइरोस्टैटिक्स की शुरुआत। श्रृंखला "प्राकृतिक विज्ञान के क्लासिक्स" जीएनटीटीआई। एम.-एल. 1933.
सापेक्षता का यांत्रिक सिद्धांत
सापेक्षता का सिद्धांत शास्त्रीय यांत्रिकी में जड़त्वीय संदर्भ प्रणालियों (आईआरएस) की समानता का सिद्धांत है, जो इस तथ्य में प्रकट होता है कि ऐसी सभी प्रणालियों में यांत्रिकी के नियम समान हैं, 1636 में जी गैलीलियो द्वारा स्थापित किया गया था।
गैलीलियो ने आराम से जहाज के डेक के नीचे होने वाली घटनाओं या समान रूप से और सीधी रेखा में (पृथ्वी के सापेक्ष, जिसे पर्याप्त सटीकता के साथ जड़त्व के रूप में माना जा सकता है) के उदाहरण का उपयोग करके जड़त्वीय प्रणालियों के लिए यांत्रिकी के नियमों की समानता का वर्णन किया संदर्भ का ढांचा): "अब जहाज को किसी भी गति से आगे बढ़ाएं और फिर (यदि केवल गति एक समान हो और एक दिशा या दूसरे में हिले बिना हो) तो आपको उल्लिखित सभी घटनाओं में थोड़ा सा भी बदलाव नहीं मिलेगा और उनमें से किसी में भी नहीं क्या आप यह निर्धारित करने में सक्षम होंगे कि जहाज चल रहा है या स्थिर खड़ा है... किसी कामरेड पर कोई चीज़ फेंकते समय, जब वह धनुष पर हो और आप कड़ी स्थिति में हों तो आपको इसे अधिक बल से नहीं फेंकना होगा, जब आपके रिश्तेदार स्थिति में हों उलटे हैं; बूंदें, पहले की तरह, निचले जहाज में गिरेंगी, और एक भी बूंद स्टर्न के करीब नहीं गिरेगी, हालांकि जब बूंद हवा में होगी, जहाज कई स्पैन की यात्रा करेगा" ("दो सबसे महत्वपूर्ण प्रणालियों पर संवाद द वर्ल्ड, टॉलेमिक और कोपर्निकन," एम. - एल., 1948, पृष्ठ 147)।
किसी भौतिक बिंदु की सापेक्ष गति: इसकी स्थिति, गति, प्रक्षेपवक्र का प्रकार इस बात पर निर्भर करता है कि इस गति को किस संदर्भ प्रणाली (संदर्भ निकाय) के संबंध में माना जाता है। साथ ही, शास्त्रीय यांत्रिकी के नियम, यानी, संबंध जो भौतिक बिंदुओं की गति और उनके बीच की बातचीत का वर्णन करने वाली मात्राओं को जोड़ते हैं, सभी जड़त्वीय संदर्भ प्रणालियों में समान हैं। यांत्रिक गति की सापेक्षता और संदर्भ के विभिन्न जड़त्वीय फ्रेमों में यांत्रिकी के नियमों की समानता (अप्रासंगिकता) गैलीलियो के सापेक्षता के सिद्धांत की सामग्री का गठन करती है। सिद्धांत स्वयं गैलीलियो के प्रसिद्ध परिवर्तनों से तार्किक रूप से अनुसरण करता है।
गैलीलियो के परिवर्तन– एक जड़त्वीय संदर्भ प्रणाली से संक्रमण करते समय निर्देशांक और वेग के परिवर्तन के शास्त्रीय यांत्रिकी में(आईएसओ)दूसरे करने के लिए.
ये परिवर्तन केवल निर्वात में प्रकाश की गति से बहुत कम गति पर मान्य हैं और दो मान्यताओं पर आधारित हैं जिन्हें स्पष्ट रूप से स्वीकार किया गया था और स्पष्ट माना गया था:
संदर्भ के सभी जड़त्वीय ढाँचों में समय बीतने का क्रम समान है;
किसी पिंड के रैखिक आयाम संदर्भ प्रणाली के सापेक्ष उसकी गति की गति पर निर्भर नहीं करते हैं।
 चावल। 80. चावल। 80. |
मान लीजिए कि दो जड़त्वीय संदर्भ प्रणालियाँ हैं, जिनमें से एक, हम आराम से विचार करने के लिए सहमत हैं; दूसरी प्रणाली, स्थिर गति से चलती है जैसा कि चित्र में दिखाया गया है। 80.
तब गैलीलियन परिवर्तनों का रूप इस प्रकार है:
या, वेक्टर संकेतन का उपयोग करते हुए,
(अंतिम सूत्र निर्देशांक अक्षों की किसी भी दिशा के लिए सत्य रहता है)।
गैलीलियो के परिवर्तनों से यह इस प्रकार है:
वेग जोड़ने का शास्त्रीय नियम: एक बिंदु की गति कहां है एमएक "निश्चित" संदर्भ फ़्रेम में, ’ - चलती प्रणाली में बिंदु एम की गति;
किसी बिंदु के त्वरण की अपरिवर्तनीयता (स्थिरता)। एमऔर उस पर कार्य करने वाली ताकतें:
अंतिम संबंधों से यह निष्कर्ष निकलता है कि एक आईएसओ से दूसरे आईएसओ पर जाने पर न्यूटन के दूसरे नियम का समीकरण नहीं बदलता है, अर्थात। गैलीलियन परिवर्तनों के लिए न्यूटन के नियम अपरिवर्तनीय हैं।
सापेक्षता के शास्त्रीय सिद्धांत के आधुनिक सूत्रीकरण:
1). सभी आईएसओ में समान परिस्थितियों में, सभी यांत्रिक घटनाएं समान तरीके से घटित होती हैं।
2). एक आईएसओ से दूसरे आईएसओ में संक्रमण के संबंध में शास्त्रीय यांत्रिकी के नियम अपरिवर्तनीय हैं।
आधुनिक भौतिकी में यह दिखाया गया है कि सापेक्षता का शास्त्रीय सिद्धांत इंगित करता है कि सभी आईएसओ समान हैं; संदर्भ का कोई "पूर्ण" फ्रेम नहीं है।
गैलीलियो का सापेक्षता का सिद्धांत केवल शास्त्रीय यांत्रिकी में मान्य है, जो प्रकाश की गति से बहुत कम वेग वाली गतियों पर विचार करता है। प्रकाश की गति के करीब गति पर, पिंडों की गति आइंस्टीन के सापेक्षतावादी यांत्रिकी के नियमों का पालन करती है , जो निर्देशांक और लोरेंत्ज़ समय के अन्य परिवर्तनों के संबंध में अपरिवर्तनीय हैं। विशेष सिद्धांत के सिद्धांतों में से एक आइंस्टीन द्वारा तैयार किया गया था सापेक्षता का सापेक्षिक सिद्धांत: एक आईएसओ से दूसरे आईएसओ में संक्रमण के संबंध में भौतिकी के नियम अपरिवर्तनीय हैं।
घर्षण बल हमेशा संपर्क सतह के साथ गति के विपरीत दिशा में निर्देशित होता है। यह हमेशा सामान्य दबाव के बल से कम होता है।
यहाँ:
एफ- गुरुत्वाकर्षण बल जिससे दो पिंड एक दूसरे को आकर्षित करते हैं (न्यूटन),
मी 1- पहले पिंड का द्रव्यमान (किलो),
मी 2- दूसरे पिंड का द्रव्यमान (किलो),
आर- पिंडों के द्रव्यमान केंद्रों के बीच की दूरी (मीटर),
γ
- गुरुत्वाकर्षण स्थिरांक 6.67 10 -11 (एम 3 /(किग्रा सेकंड 2)),
गुरुत्वाकर्षण क्षेत्र की ताकत- एक वेक्टर मात्रा जो किसी दिए गए बिंदु पर गुरुत्वाकर्षण क्षेत्र को दर्शाती है और संख्यात्मक रूप से क्षेत्र में किसी दिए गए बिंदु पर रखे गए शरीर पर कार्य करने वाले गुरुत्वाकर्षण बल और इस शरीर के गुरुत्वाकर्षण द्रव्यमान के अनुपात के बराबर होती है:
12. कठोर शरीर यांत्रिकी का अध्ययन करते समय, हमने बिल्कुल कठोर शरीर की अवधारणा का उपयोग किया। लेकिन प्रकृति में बिल्कुल ठोस पिंड नहीं होते, क्योंकि... सभी वास्तविक पिंड, बलों के प्रभाव में, अपना आकार और आकार बदलते हैं, अर्थात। विकृत.
विरूपणबुलाया लोचदार, यदि, बाहरी शक्तियों के शरीर पर कार्य करना बंद करने के बाद, शरीर अपने मूल आकार और आकृति को पुनः प्राप्त कर लेता है। बाह्य शक्तियों के समाप्त होने के बाद शरीर में जो विकृतियाँ रह जाती हैं, वे कहलाती हैं प्लास्टिक(या अवशिष्ट)
संचालन और शक्ति
बल का कार्य.
एक सीधी रेखा में गतिशील वस्तु पर कार्य करने वाले स्थिर बल द्वारा किया गया कार्य
, शरीर का विस्थापन कहां है, शरीर पर लगने वाला बल है। 
सामान्य तौर पर, एक घुमावदार पथ पर चलते हुए किसी पिंड पर कार्य करने वाले परिवर्तनशील बल द्वारा किया गया कार्य  . कार्य को जूल [जे] में मापा जाता है।
. कार्य को जूल [जे] में मापा जाता है।
एक निश्चित अक्ष के चारों ओर घूम रहे किसी पिंड पर लगने वाले बल के क्षण का कार्य, जहां बल का क्षण है और घूर्णन का कोण है।
सामान्य रूप में ।
शरीर द्वारा किया गया कार्य उसकी गतिज ऊर्जा में बदल जाता है।
शक्ति- यह समय की प्रति इकाई कार्य है (1 सेकंड): . शक्ति को वाट्स [डब्ल्यू] में मापा जाता है।
14.गतिज ऊर्जा- एक यांत्रिक प्रणाली की ऊर्जा, उसके बिंदुओं की गति की गति पर निर्भर करती है। स्थानांतरीय और घूर्णी गति की गतिज ऊर्जा अक्सर जारी होती है।
आइए एक कण से युक्त प्रणाली पर विचार करें और न्यूटन का दूसरा नियम लिखें:
किसी पिंड पर कार्य करने वाली सभी शक्तियों का परिणाम होता है। आइए हम समीकरण को कण के विस्थापन से गुणा करें। उस पर विचार करते हुए, हमें मिलता है:

यदि सिस्टम बंद है, अर्थात  , और मूल्य
, और मूल्य
स्थिर रहता है। यह मात्रा कहलाती है गतिज ऊर्जाकण. यदि सिस्टम पृथक है, तो गतिज ऊर्जा गति का अभिन्न अंग है।
एक बिल्कुल कठोर शरीर के लिए, कुल गतिज ऊर्जा को स्थानान्तरणीय और घूर्णी गति की गतिज ऊर्जा के योग के रूप में लिखा जा सकता है:
![]()
शरीर का भार
शरीर के द्रव्यमान केंद्र की गति
शरीर की जड़ता का क्षण
शरीर का कोणीय वेग.
15.संभावित ऊर्जा- एक अदिश भौतिक मात्रा जो बलों की कार्रवाई के क्षेत्र में अपनी उपस्थिति के कारण एक निश्चित शरीर (या भौतिक बिंदु) की कार्य करने की क्षमता को दर्शाती है।
16. स्प्रिंग को खींचने या संपीड़ित करने से इसकी लोचदार विरूपण की संभावित ऊर्जा का भंडारण होता है। स्प्रिंग की संतुलन स्थिति में वापसी के परिणामस्वरूप संग्रहीत लोचदार विरूपण ऊर्जा जारी होती है। इस ऊर्जा का परिमाण है:
 लोचदार विरूपण की संभावित ऊर्जा..
लोचदार विरूपण की संभावित ऊर्जा..
 - लोचदार बल का कार्य और लोचदार विरूपण की संभावित ऊर्जा में परिवर्तन।
- लोचदार बल का कार्य और लोचदार विरूपण की संभावित ऊर्जा में परिवर्तन।
17.रूढ़िवादी ताकतें(संभावित बल) - वे बल जिनका कार्य प्रक्षेपवक्र के आकार पर निर्भर नहीं करता है (केवल बलों के अनुप्रयोग के आरंभ और समाप्ति बिंदुओं पर निर्भर करता है)। इससे परिभाषा का तात्पर्य है: रूढ़िवादी बल वे बल हैं जिनका किसी भी बंद प्रक्षेपवक्र पर कार्य 0 के बराबर होता है
विघटनकारी ताकतें- बल, जिसके प्रभाव में एक यांत्रिक प्रणाली पर, इसकी कुल यांत्रिक ऊर्जा कम हो जाती है (अर्थात समाप्त हो जाती है), ऊर्जा के अन्य, गैर-यांत्रिक रूपों में बदल जाती है, उदाहरण के लिए, गर्मी में।
18. एक निश्चित अक्ष के चारों ओर घूमनायह एक कठोर पिंड की गति है जिसमें पूरी गति के दौरान इसके दो बिंदु गतिहीन रहते हैं। इन बिंदुओं से गुजरने वाली सीधी रेखा को घूर्णन अक्ष कहा जाता है। पिंड के अन्य सभी बिंदु घूर्णन अक्ष के लंबवत् तलों में, उन वृत्तों के अनुदिश गति करते हैं जिनके केंद्र घूर्णन अक्ष पर स्थित होते हैं।
निष्क्रियता के पल- एक अदिश भौतिक राशि, एक अक्ष के चारों ओर घूर्णी गति में जड़ता का एक माप, जैसे किसी पिंड का द्रव्यमान अनुवादात्मक गति में उसकी जड़ता का एक माप है। यह शरीर में द्रव्यमान के वितरण की विशेषता है: जड़ता का क्षण आधार सेट (बिंदु, रेखा या विमान) से उनकी दूरी के वर्ग द्वारा प्राथमिक द्रव्यमान के उत्पादों के योग के बराबर है।
एक यांत्रिक प्रणाली की जड़ता का क्षणएक निश्चित अक्ष के सापेक्ष ("जड़ता का अक्षीय क्षण") मात्रा है जे ए, सभी के द्रव्यमान के उत्पादों के योग के बराबर एनसिस्टम के भौतिक बिंदु अक्ष से उनकी दूरी के वर्गों द्वारा:
![]() ,
,
§ एम मैं- वज़न मैंवां बिंदु,
§ आर मैं- से दूरी मैंवें अक्ष को इंगित करता है।
AXIAL निष्क्रियता के पलशरीर जे एएक अक्ष के चारों ओर घूर्णी गति में किसी पिंड की जड़ता का एक माप है, जैसे किसी पिंड का द्रव्यमान अनुवादात्मक गति में उसकी जड़ता का एक माप है।
 ,
,
§ - शरीर के आयतन के एक छोटे तत्व का द्रव्यमान,
द्रव्यमान के केंद्र से गुजरने वाली कुछ अक्षों के चारों ओर घूमने वाला एक कठोर पिंड, यदि बाहरी प्रभावों से मुक्त हो जाता है, तो अनिश्चित काल तक घूर्णन बनाए रखता है. (यह निष्कर्ष अनुवादात्मक गति के लिए न्यूटन के पहले नियम के समान है।)
किसी कठोर पिंड के घूमने की घटना हमेशा शरीर के अलग-अलग बिंदुओं पर लागू बाहरी बलों की कार्रवाई के कारण होती है। इस मामले में, विकृतियों की घटना और आंतरिक बलों की उपस्थिति अपरिहार्य है, जो एक ठोस शरीर के मामले में इसके आकार के व्यावहारिक संरक्षण को सुनिश्चित करती है। जब बाहरी बलों की कार्रवाई बंद हो जाती है, तो घूर्णन संरक्षित रहता है: आंतरिक बल किसी कठोर पिंड के घूर्णन का न तो कारण बन सकते हैं और न ही उसे नष्ट कर सकते हैं।
घूर्णन की एक निश्चित धुरी वाले पिंड पर बाहरी बल की कार्रवाई का परिणाम पिंड की त्वरित घूर्णी गति है. (यह निष्कर्ष अनुवादात्मक गति के लिए न्यूटन के दूसरे नियम के समान है।)
घूर्णी गति की गतिशीलता का मूल नियम: एक जड़त्वीय संदर्भ फ्रेम में, एक निश्चित अक्ष के चारों ओर घूमने वाले शरीर द्वारा प्राप्त कोणीय त्वरण शरीर पर कार्य करने वाले सभी बाहरी बलों के कुल क्षण के समानुपाती होता है, और किसी दिए गए अक्ष के सापेक्ष शरीर की जड़ता के क्षण के व्युत्क्रमानुपाती होता है। :
एक सरल सूत्रीकरण दिया जा सकता है घूर्णी गति की गतिशीलता का मूल नियम(इसे भी कहा जाता है घूर्णी गति के लिए न्यूटन का दूसरा नियम): टॉर्क जड़ता के क्षण और कोणीय त्वरण के उत्पाद के बराबर है:
आवेग का क्षण(कोनेदार गति, कोनेदार गति) किसी पिंड के जड़त्व आघूर्ण और कोणीय वेग का गुणनफल कहलाता है:
संवेग एक सदिश राशि है. इसकी दिशा कोणीय वेग वेक्टर की दिशा से मेल खाती है।
कोणीय संवेग में परिवर्तन निम्नानुसार निर्धारित किया जाता है:
![]() . (आई.112)
. (आई.112)
कोणीय गति में परिवर्तन (पिंड की जड़ता के एक स्थिर क्षण के साथ) केवल कोणीय वेग में परिवर्तन के परिणामस्वरूप हो सकता है और हमेशा बल के एक क्षण की क्रिया के कारण होता है।
सूत्र के अनुसार, साथ ही सूत्र (I.110) और (I.112) के अनुसार, कोणीय गति में परिवर्तन को इस प्रकार दर्शाया जा सकता है:
![]() . (आई.113)
. (आई.113)
सूत्र (I.113) में उत्पाद को कहा जाता है संवेग आवेग या प्रेरक शक्ति. यह कोणीय गति में परिवर्तन के बराबर है।
फॉर्मूला (I.113) मान्य है बशर्ते कि बल का क्षण समय के साथ न बदले। यदि बल का क्षण समय पर निर्भर करता है, अर्थात , वह
 . (आई.114)
. (आई.114)
सूत्र (I.114) से पता चलता है कि: कोणीय संवेग में परिवर्तन बल के क्षण के समय अभिन्न अंग के बराबर होता है. इसके अलावा, यदि इस सूत्र को इस रूप में प्रस्तुत किया जाता है:, तो परिभाषा इससे अनुसरण करेगी बल का क्षण: तात्कालिक बलाघूर्ण समय के संबंध में कोणीय गति का पहला व्युत्पन्न है,