Cómo encontrar una recta en un triángulo. ¿Cómo encontrar la línea media de un triángulo? Propiedades, definiciones y métodos básicos.

1 Construcción adicional que conduce al teorema de la línea media del triángulo, al trapezoide y a las propiedades de similitud de los triángulos.

Y ella igual a la mitad de la hipotenusa.
Corolario 1.
Corolario 2.

De esto queda claro que

1 Todos los triángulos rectángulos con el mismo ángulo agudo son semejantes. Una mirada a las funciones trigonométricas.

Los triángulos con lados sombreados y no sombreados son similares en que sus dos ángulos son iguales. Por lo tanto donde

Esto significa que las relaciones indicadas dependen únicamente del ángulo agudo del triángulo rectángulo y esencialmente lo determinan. Ésta es una de las razones de la aparición de funciones trigonométricas:

¡A menudo escribir funciones trigonométricas de ángulos en triángulos rectángulos similares es más claro que escribir relaciones de similitud!

Bajemos la altura CH a la hipotenusa AB. Tenemos tres triángulos semejantes ABC, AHC y CHB. Escribamos expresiones para funciones trigonométricas:

De esto queda claro que . Sumando, obtenemos el teorema de Pitágoras, ya que:

Para otra demostración del teorema de Pitágoras, consulte el comentario al problema 4.
3 Un ejemplo importante de una construcción adicional es la construcción de un ángulo igual a uno de los ángulos de un triángulo.

Desde el vértice del ángulo recto trazamos un segmento de recta que forma un ángulo con el cateto CA igual al ángulo CAB del triángulo rectángulo dado ABC. Como resultado, obtenemos un triángulo isósceles ACM con ángulos base. Pero el otro triángulo resultante de esta construcción también será isósceles, ya que cada uno de sus ángulos en la base es igual (por la propiedad de los ángulos de un triángulo rectángulo y por construcción - el ángulo fue "restado" del ángulo recto). Debido a que los triángulos BMC y AMC son isósceles con lado común MC, tenemos la igualdad MB=MA=MC, es decir MC mediana trazada a la hipotenusa de un triángulo rectángulo, y ella igual a la mitad de la hipotenusa.
Corolario 1. El punto medio de la hipotenusa es el centro del círculo circunscrito a este triángulo, ya que resulta que el punto medio de la hipotenusa equidista de los vértices del triángulo rectángulo.
Corolario 2. La línea media de un triángulo rectángulo, que conecta la mitad de la hipotenusa y la mitad del cateto, es paralela al cateto opuesto y es igual a la mitad del mismo.

En los triángulos isósceles BMC y AMC, bajemos las alturas MH y MG a las bases. Dado que en un triángulo isósceles la altura bajada a la base también es la mediana (y la bisectriz), entonces MH y MG son las líneas de un triángulo rectángulo que conectan la mitad de la hipotenusa con los puntos medios de los catetos. Por construcción, resultan ser paralelos a los catetos opuestos e iguales a sus mitades, ya que los triángulos son iguales MHC y MGC son iguales (y MHCG es un rectángulo). Este resultado es la base para la demostración del teorema sobre la línea media de un triángulo arbitrario y, además, la línea media de un trapezoide y la propiedad de proporcionalidad de los segmentos cortados por líneas paralelas en dos rectas que los cortan.

Tareas
Usando propiedades de similitud -1
Usando propiedades básicas - 2
Usando formación adicional 3-4

1 2 3 4

La altura caída desde el vértice de un ángulo recto de un triángulo rectángulo es igual a la raíz cuadrada de las longitudes de los segmentos en los que divide la hipotenusa.

La solución parece obvia si se conoce la derivación del teorema de Pitágoras a partir de la semejanza de triángulos:

\(\mathrm(tg)\beta=\frac(h)(c_1)=\frac(c_2)(h)\),
de donde \(h^2=c_1c_2\).

Encuentre el lugar geométrico de los puntos (GMT) de intersección de las medianas de todos los triángulos rectángulos posibles cuya hipotenusa AB es fija.

El punto de intersección de las medianas de cualquier triángulo corta un tercio de la mediana, contando desde el punto de su intersección con el lado correspondiente. En un triángulo rectángulo, la mediana trazada desde el ángulo recto es igual a la mitad de la hipotenusa. Por lo tanto, el GMT deseado es un círculo de radio igual a 1/6 de la longitud de la hipotenusa, con un centro en el medio de esta hipotenusa (fija).

La línea media del triángulo. ¡Hola amigos! Hoy existe material teórico, está relacionado con el triángulo. El examen contiene un grupo de tareas que utilizan la propiedad de su línea media. Y no sólo en problemas de triángulos, sino también de trapecios. Hubo uno en el que sugerí simplemente recordar estos hechos, ahora con más detalle...

¿Qué es la línea media de un triángulo y cuáles son sus propiedades?

Definición. La línea media de un triángulo es un segmento que conecta los puntos medios de los lados del triángulo.

Está claro que hay tres líneas medias en el triángulo. Mostrémosles:

Sin ninguna prueba, probablemente ya habrás notado que los cuatro triángulos formados son iguales. Esto es cierto, pero hablaremos de ello con más detalle más adelante.

Teorema. La línea media de un triángulo que conecta los puntos medios de dos lados dados es paralela al tercer lado e igual a la mitad de este.

Prueba:

1. Miremos los triángulos BMN y BAC. Según la condición, tenemos BM=MA, BN=NC. Podemos escribir:

Por tanto, los triángulos son semejantes en dos lados proporcionales y en el ángulo entre ellos (el segundo signo de semejanza). ¿Qué se sigue de esto? Pero el hecho de que:

Basado en el paralelismo de las rectas MN||AC.

2. También de la similitud de los triángulos se deduce que

Es decir, MN es dos veces menor. ¡Probado!

Resolvamos un problema típico.

En el triángulo ABC, los puntos M, N, K son los puntos medios de los lados AB, BC, AC. Encuentra el perímetro del triángulo ABC si MN=12, MK=10, KN=8.

Solución. Por supuesto, antes que nada deberías comprobar la existencia del triángulo MNK (y por tanto la existencia del triángulo ABC). La suma de los dos lados menores debe ser mayor que el tercer lado, escribe 10+8>12. Se cumplirá, por eso existe el triángulo.

Construyamos un boceto:

Por tanto, el perímetro del triángulo ABC es 24+20+16=60.

*Ahora más detalles sobre los triángulos obtenidos al construir las tres líneas medias. Su igualdad se prueba fácilmente. Mirar:

Son iguales en tres lados. Por supuesto, aquí también se aplican otras señales. lo entendemos

¿Cómo se utiliza esta propiedad en las tareas incluidas en el examen? Me gustaría centrarme especialmente en los problemas de estereometría. Hay tipos en los que hablamos de un prisma triangular.

Por ejemplo, se dice que el plano pasa por los puntos medios de los lados de la base y es paralelo al tercer borde de la base. Surgen interrogantes sobre cambios en la superficie del prisma, su volumen y otros.

Asi que aqui esta. Conociendo y comprendiendo la información presentada anteriormente, determinará inmediatamente que este plano corta una cuarta parte de la base del prisma especificado y resolverá el problema de forma oral. Con tales tareas.

¡Eso es todo! ¡Mis mejores deseos!

Descargar material del artículo

Atentamente, Alexander Krutitskikh.

A veces, es posible que los temas que se explican en la escuela no siempre queden claros la primera vez. Esto es especialmente cierto para una materia como las matemáticas. Pero todo se complica mucho más cuando esta ciencia comienza a dividirse en dos partes: álgebra y geometría.

Cada estudiante puede tener una habilidad en una de dos áreas, pero especialmente en los grados de primaria es importante comprender las bases tanto del álgebra como de la geometría. En geometría, se considera que uno de los temas principales es la sección de triángulos.

¿Cómo encontrar la línea media de un triángulo? Vamos a resolverlo.

Conceptos básicos

Para empezar, para descubrir cómo encontrar la línea media de un triángulo, es importante entender qué es.

No hay restricciones para dibujar la línea media: el triángulo puede ser cualquier cosa (isosceles, equilátero, rectangular). Y todas las propiedades que se relacionen con la línea media estarán vigentes.

La línea media de un triángulo es un segmento que conecta los puntos medios de sus 2 lados. Por lo tanto, cualquier triángulo puede tener 3 de esas líneas.

Propiedades

Para saber cómo encontrar la línea media de un triángulo, designemos sus propiedades que deben recordarse, de lo contrario sin ellas será imposible resolver problemas con la necesidad de designar la longitud de la línea media, ya que todos los datos obtenidos deben ser fundamentados. y argumentó con teoremas, axiomas o propiedades.

Así, para responder a la pregunta: “¿Cómo encontrar la línea media del triángulo ABC?”, basta con conocer uno de los lados del triángulo.

Pongamos un ejemplo.

Echa un vistazo a la imagen. Muestra el triángulo ABC con la línea media DE. Tenga en cuenta que es paralelo a la base AC en el triángulo. Por lo tanto, cualquiera que sea el valor de AC, la línea promedio DE será la mitad de grande. Por ejemplo, AC=20 significa DE=10, etc.

De estas sencillas formas podrás entender cómo encontrar la línea media de un triángulo. Recuerda sus propiedades básicas y su definición, y entonces nunca tendrás problemas para encontrar su significado.

\[(\Large(\text(Similitud de triángulos)))\]

Definiciones

Dos triángulos se llaman semejantes si sus ángulos son respectivamente iguales y los lados de un triángulo son proporcionales a los lados semejantes del otro.
(Los lados se llaman similares si se encuentran frente a ángulos iguales).

El coeficiente de similitud de triángulos (similares) es un número igual a la razón de los lados similares de estos triángulos.

Definición

El perímetro de un triángulo es la suma de las longitudes de todos sus lados.

Teorema

La razón de los perímetros de dos triángulos semejantes es igual al coeficiente de similitud.

Prueba

Considere los triángulos \(ABC\) y \(A_1B_1C_1\) con lados \(a,b,c\) y \(a_1, b_1, c_1\) respectivamente (ver figura arriba).

Entonces \(P_(ABC)=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_(A_1B_1C_1)\)

Teorema

La razón de las áreas de dos triángulos semejantes es igual al cuadrado del coeficiente de similitud.

Prueba

Sean semejantes los triángulos \(ABC\) y \(A_1B_1C_1\), y \(\dfrac(AB)(A_1B_1) = \dfrac(AC)(A_1C_1) = \dfrac(BC)(B_1C_1) = k\). Denotemos con las letras \(S\) y \(S_1\) las áreas de estos triángulos, respectivamente.

Dado que \(\angle A = \angle A_1\) , entonces \(\dfrac(S)(S_1) = \dfrac(AB\cdot AC)(A_1B_1\cdot A_1C_1)\)(por el teorema de la razón de las áreas de triángulos que tienen ángulos iguales).

Porque \(\dfrac(AB)(A_1B_1) = \dfrac(AC)(A_1C_1) = k\), Eso \(\dfrac(S)(S_1) = \dfrac(AB)(A_1B_1)\cdot\dfrac(AC)(A_1C_1) = k\cdot k = k^2\), que era lo que había que demostrar.

\[(\Large(\text(Signos de similitud de triángulos)))\]

Teorema (el primer signo de similitud de triángulos)

Si dos ángulos de un triángulo son respectivamente iguales a dos ángulos de otro triángulo, entonces dichos triángulos son semejantes.

Prueba

Sean \(ABC\) y \(A_1B_1C_1\) triángulos tales que \(\angle A = \angle A_1\) , \(\angle B = \angle B_1\) . Entonces, por el teorema de la suma de los ángulos de un triángulo \(\angle C = 180^\circ - \angle A - \angle B = 180^\circ - \angle A_1 - \angle B_1 = \angle C_1\), es decir, los ángulos del triángulo \(ABC\) son respectivamente iguales a los ángulos del triángulo \(A_1B_1C_1\) .

Dado que \(\angle A = \angle A_1\) y \(\angle B = \angle B_1\) , entonces \(\dfrac(S_(ABC))(S_(A_1B_1C_1)) = \dfrac(AB\cdot AC)(A_1B_1\cdot A_1C_1)\) Y \(\dfrac(S_(ABC))(S_(A_1B_1C_1)) = \dfrac(AB\cdot BC)(A_1B_1\cdot B_1C_1)\).

De estas igualdades se deduce que \(\dfrac(AC)(A_1C_1) = \dfrac(BC)(B_1C_1)\).

De la misma manera, se demuestra que \(\dfrac(AC)(A_1C_1) = \dfrac(AB)(A_1B_1)\)(usando igualdades \(\angle B = \angle B_1\) , \(\angle C = \angle C_1\) ).

Como resultado, los lados del triángulo \(ABC\) son proporcionales a los lados similares del triángulo \(A_1B_1C_1\), que es lo que había que demostrar.

Teorema (segundo criterio para la similitud de triángulos)

Si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos entre estos lados son iguales, entonces los triángulos son semejantes.

Prueba

Considere dos triángulos \(ABC\) y \(A"B"C"\) tales que \(\dfrac(AB)(A"B")=\dfrac(AC)(A"C")\), \(\angle BAC = \angle A"\) Demostremos que los triángulos \(ABC\) y \(A"B"C"\) son semejantes. Teniendo en cuenta el primer signo de semejanza de los triángulos, basta con demostrar que \(\angle B = \angle B"\) .

Considere un triángulo \(ABC""\) con \(\angle 1 = \angle A"\) , \(\angle 2 = \angle B"\) . Los triángulos \(ABC""\) y \(A"B"C"\) son similares según el primer criterio de similitud de triángulos, entonces \(\dfrac(AB)(A"B") = \dfrac(AC"")(A"C")\).

Por otro lado, por condición \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C")\). De las dos últimas igualdades se deduce que \(AC = AC""\) .

Los triángulos \(ABC\) y \(ABC""\) son iguales en dos lados y el ángulo entre ellos, por lo tanto, \(\ángulo B = \ángulo 2 = \ángulo B"\).

Teorema (tercer signo de semejanza de triángulos)

Si tres lados de un triángulo son proporcionales a tres lados de otro triángulo, entonces los triángulos son semejantes.

Prueba

Sean proporcionales los lados de los triángulos \(ABC\) y \(A"B"C"\): \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C") = \dfrac(BC)(B"C")\). Demostremos que los triángulos \(ABC\) y \(A"B"C"\) son semejantes.

Para ello, teniendo en cuenta el segundo criterio de similitud de triángulos, basta con demostrar que \(\angle BAC = \angle A"\) .

Considere un triángulo \(ABC""\) con \(\angle 1 = \angle A"\) , \(\angle 2 = \angle B"\) .

Los triángulos \(ABC""\) y \(A"B"C"\) son similares según el primer criterio de similitud de triángulos, por lo tanto, \(\dfrac(AB)(A"B") = \dfrac(BC"")(B"C") = \dfrac(C""A)(C"A")\).

De la última cadena de igualdades y condiciones. \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C") = \dfrac(BC)(B"C")\) se deduce que \(BC = BC""\) , \(CA = C""A\) .

Los triángulos \(ABC\) y \(ABC""\) son iguales en tres lados, por lo tanto, \(\ángulo BAC = \ángulo 1 = \ángulo A"\).

\[(\Large(\text(Teorema de Tales)))\]

Teorema

Si marca segmentos iguales en un lado de un ángulo y dibuja líneas rectas paralelas a través de sus extremos, estas líneas rectas también cortarán segmentos iguales en el otro lado.

Prueba

Probemos primero lema: Si en \(\triangle OBB_1\) se traza una línea recta \(a\parallel BB_1\) que pasa por el medio \(A\) del lado \(OB\), entonces también cortará al lado \(OB_1\) en la mitad.

Por el punto \(B_1\) dibujamos \(l\parallel OB\) . Sea \(l\cap a=K\) . Entonces \(ABB_1K\) es un paralelogramo, por lo tanto \(B_1K=AB=OA\) y \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\); \(\ángulo AA_1O=\ángulo KA_1B_1\) como vertical. Entonces, según el segundo signo. \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\). El lema está probado.

Pasemos a la demostración del teorema. Sea \(OA=AB=BC\) , \(a\parallel b\parallel c\) y necesitamos demostrar que \(OA_1=A_1B_1=B_1C_1\) .

Así, según este lema \(OA_1=A_1B_1\) . Demostremos que \(A_1B_1=B_1C_1\) . Dibujemos una recta \(d\parallel OC\) que pase por el punto \(B_1\), y sea \(d\cap a=D_1, d\cap c=D_2\) . Entonces \(ABB_1D_1, BCD_2B_1\) son paralelogramos, por lo tanto, \(D_1B_1=AB=BC=B_1D_2\) . De este modo, \(\ángulo A_1B_1D_1=\ángulo C_1B_1D_2\) como vertical \(\ángulo A_1D_1B_1=\ángulo C_1D_2B_1\) yaciendo como cruces, y, por lo tanto, según el segundo signo \(\triangle A_1B_1D_1=\triangle C_1B_1D_2 \Rightarrow A_1B_1=B_1C_1\).

teorema de tales

Las rectas paralelas cortan segmentos proporcionales a los lados de un ángulo.

Prueba

Deja líneas paralelas \(p\paralelo q\paralelo r\paralelo s\) dividió una de las líneas en segmentos \(a, b, c, d\) . Luego, la segunda línea recta debe dividirse en segmentos \(ka, kb, kc, kd\), respectivamente, donde \(k\) es un cierto número, el mismo coeficiente de proporcionalidad de los segmentos.

Dibujemos por el punto \(A_1\) una recta \(p\parallel OD\) (\(ABB_2A_1\) es un paralelogramo, por lo tanto, \(AB=A_1B_2\) ). Entonces \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) en dos esquinas. Por eso, \(\dfrac(OA)(A_1B_2)=\dfrac(OA_1)(A_1B_1) \Rightarrow A_1B_1=kb\).

De manera similar, trazamos una línea recta que pasa por \(B_1\) \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) etc.

\[(\Large(\text(Línea media del triángulo)))\]

Definición

La línea media de un triángulo es un segmento que conecta los puntos medios de dos lados cualesquiera del triángulo.

Teorema

La línea media del triángulo es paralela al tercer lado e igual a la mitad del mismo.

Prueba

1) El paralelismo de la línea media con la base se desprende de lo demostrado anteriormente. lemas.

2) Demostremos que \(MN=\dfrac12 AC\) .

Por el punto \(N\) trazamos una recta paralela a \(AB\) . Deje que esta línea cruce el lado \(AC\) en el punto \(K\) . Entonces \(AMNK\) es un paralelogramo ( \(AM\paralelo NK, MN\paralelo AK\) según el punto anterior). Entonces, \(MN=AK\) .

Porque \(NK\parallel AB\) y \(N\) son el punto medio de \(BC\), luego, según el teorema de Tales, \(K\) es el punto medio de \(AC\). Por lo tanto, \(MN=AK=KC=\dfrac12 AC\) .

Consecuencia

La línea media del triángulo corta de ella un triángulo similar al dado con el coeficiente \(\frac12\) .

Un cuadrilátero en el que sólo dos lados son paralelos se llama trapezoide.

Los lados paralelos de un trapezoide se llaman sus razones, y aquellos lados que no son paralelos se llaman lados. Si los lados son iguales, entonces dicho trapezoide es isósceles. La distancia entre las bases se llama altura del trapezoide.

Trapezoide de línea media

La línea media es un segmento que conecta los puntos medios de los lados del trapezoide. La línea media del trapezoide es paralela a sus bases.

Teorema:

Si la línea recta que cruza el centro de un lado es paralela a las bases del trapezoide, entonces biseca el segundo lado del trapezoide.

Teorema:

La longitud de la línea media es igual a la media aritmética de las longitudes de sus bases.

MN línea media, AB y CD - bases, AD y BC - lados laterales

MN = (AB + DC)/2

Teorema:

La longitud de la línea media de un trapezoide es igual a la media aritmética de las longitudes de sus bases.

La tarea principal: Demuestre que la línea media de un trapezoide biseca un segmento cuyos extremos se encuentran en el medio de las bases del trapezoide.

Línea media del triángulo

El segmento que une los puntos medios de dos lados de un triángulo se llama línea media del triángulo. Es paralelo al tercer lado y su longitud es igual a la mitad de la longitud del tercer lado.
Teorema: Si una línea que corta el punto medio de un lado de un triángulo es paralela al otro lado del triángulo, entonces biseca el tercer lado.

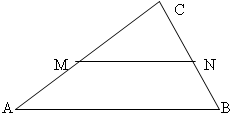
AM = MC y BN = NC =>

Aplicar las propiedades de la línea media de un triángulo y un trapezoide.

Dividir un segmento en un número determinado de partes iguales.
Tarea: Divida el segmento AB en 5 partes iguales.
Solución:
Sea p un rayo aleatorio cuyo origen es el punto A y que no se encuentra en la recta AB. Reservamos secuencialmente 5 segmentos iguales en p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 ​​​​A 5
Conectamos A 5 con B y trazamos líneas a través de A 4, A 3, A 2 y A 1 que son paralelas a A 5 B. Se cruzan con AB respectivamente en los puntos B 4, B 3, B 2 y B 1. Estos puntos dividen el segmento AB en 5 partes iguales. De hecho, del trapecio BB 3 A 3 A 5 vemos que BB 4 = B 4 B 3. De la misma forma, del trapezoide B 4 B 2 A 2 A 4 obtenemos B 4 B 3 = B 3 B 2

Mientras que del trapezoide B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Luego de B 2 AA 2 se deduce que B 2 B 1 = B 1 A. En conclusión obtenemos:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Está claro que para dividir el segmento AB en otro número de partes iguales, necesitamos proyectar el mismo número de segmentos iguales sobre el rayo p. Y luego continúe de la manera descrita anteriormente.