Как да намерите линия в триъгълник. Как да намерим средната линия на триъгълник? Основни свойства, определения и методи

1 Допълнителна конструкция, водеща до теоремата за средната линия на триъгълника, свойствата на трапеца и подобието на триъгълниците.

И тя равно на половината от хипотенузата.
Следствие 1.
Следствие 2.

От това става ясно, че

1 Всички правоъгълни триъгълници с еднакъв остър ъгъл са подобни. Поглед към тригонометричните функции.

Триъгълниците със щриховани и нещриховани страни си приличат по това, че двата им ъгъла са равни. Следователно къде

Това означава, че посочените отношения зависят само от острия ъгъл на правоъгълния триъгълник и по същество го определят. Това е една от причините за появата на тригонометричните функции:

Често писането на тригонометрични функции на ъгли в подобни правоъгълни триъгълници е по-ясно от писането на отношения на подобие!

Нека намалим височината CH на хипотенузата AB. Имаме три подобни триъгълника ABC, AHC и CHB. Нека напишем изрази за тригонометрични функции:

От това става ясно, че . Сумирайки, получаваме Питагоровата теорема, тъй като:

За друго доказателство на Питагоровата теорема вижте коментара към задача 4.
3 Важен пример за допълнителна конструкция е конструкцията на ъгъл, равен на един от ъглите на триъгълник.

От върха на правия ъгъл начертаваме права отсечка, която образува ъгъл с катет CA, равен на ъгъл CAB на дадения правоъгълен триъгълник ABC. В резултат на това получаваме равнобедрен триъгълник ACM с основни ъгли. Но другият триъгълник, произтичащ от тази конструкция, също ще бъде равнобедрен, тъй като всеки от неговите ъгли в основата е равен (по свойството на ъглите на правоъгълен триъгълник и по конструкция - ъгълът е „изваден“ от правия ъгъл). Поради факта, че триъгълниците BMC и AMC са равнобедрени с обща страна MC, имаме равенството MB=MA=MC, т.е. M.C. медиана, начертана към хипотенузата на правоъгълен триъгълник, и тя равно на половината от хипотенузата.
Следствие 1.Средната точка на хипотенузата е центърът на окръжността, описана около този триъгълник, тъй като се оказва, че средата на хипотенузата е на еднакво разстояние от върховете на правоъгълния триъгълник.
Следствие 2.Средната линия на правоъгълен триъгълник, свързваща средата на хипотенузата и средата на катета, е успоредна на срещуположния катет и е равна на половината от него.

В равнобедрените триъгълници BMC и AMC нека спуснем височините MH и MG към основите. Тъй като в равнобедрен триъгълник височината, спусната до основата, също е медианата (и ъглополовящата), тогава MH и MG са линиите на правоъгълен триъгълник, свързващ средата на хипотенузата със средните точки на краката. По конструкция те се оказват успоредни на противоположните крака и равни на техните половини, тъй като триъгълниците са равни MHC и MGC са равни (а MHCG е правоъгълник). Този резултат е в основата на доказателството на теоремата за средната линия на произволен триъгълник и, освен това, средната линия на трапец и свойството за пропорционалност на сегментите, отрязани от успоредни линии на две прави, които ги пресичат.

Задачи
Използване на свойства за подобие -1
Използване на основни свойства - 2
Използване на допълнителна формация 3-4

1 2 3 4

Височината, изпусната от върха на прав ъгъл на правоъгълен триъгълник, е равна на корен квадратен от дължините на сегментите, на които разделя хипотенузата.

Решението изглежда очевидно, ако знаете извеждането на Питагоровата теорема от сходството на триъгълници:

\(\mathrm(tg)\beta=\frac(h)(c_1)=\frac(c_2)(h)\),
откъдето \(h^2=c_1c_2\).

Намерете геометричното място на точките (GMT) на пресичане на медианите на всички възможни правоъгълни триъгълници, чиято хипотенуза AB е фиксирана.

Пресечната точка на медианите на всеки триъгълник отрязва една трета от медианата, считано от точката на пресичане със съответната страна. В правоъгълен триъгълник медианата, изтеглена от правия ъгъл, е равна на половината от хипотенузата. Следователно желаният GMT е кръг с радиус, равен на 1/6 от дължината на хипотенузата, с център в средата на тази (фиксирана) хипотенуза.

Средната линия на триъгълника. Здравейте приятели! Днес има теоретичен материал, той е свързан с триъгълника. Изпитът съдържа група задачи, които използват свойството средна линия. И не само в задачи с триъгълници, но и с трапеци. Имаше един, в който предложих просто да си припомним тези факти, сега по-подробно...

Каква е средната линия на триъгълник и какви са нейните свойства?

Определение.Средната линия на триъгълник е отсечка, свързваща средните точки на страните на триъгълника.

Ясно е, че в триъгълника има три средни линии. Нека им покажем:

Без никакво доказателство вероятно вече сте забелязали, че и четирите образувани триъгълника са равни. Това е вярно, но ще говорим за това по-подробно по-късно.

Теорема. Средната линия на триъгълник, свързваща средите на две дадени страни, е успоредна на третата страна и равна на половината от нея.

Доказателство:

1. Нека разгледаме триъгълниците BMN и BAC. Според условието имаме BM=MA, BN=NC. Можем да напишем:

Следователно триъгълниците са подобни по две пропорционални страни и ъгъла между тях (вторият признак за подобие). Какво следва от това? Но фактът, че:

Въз основа на успоредността на правите MN||AC.

2. Също така от подобието на триъгълниците следва, че

Тоест MN е два пъти по-малко. Доказано!

Нека решим един типичен проблем.

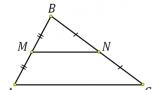
В триъгълник ABC точките M, N, K са среди на страните AB, BC, AC. Намерете периметъра на триъгълник ABC, ако MN=12, MK=10, KN=8.

Решение. Разбира се, първо трябва да проверите съществуването на триъгълник MNK (и следователно съществуването на триъгълник ABC). Сумата от двете по-малки страни трябва да е по-голяма от третата страна, напишете 10+8>12. Ще се изпълни, следователно триъгълникът съществува.

Нека изградим скица:

Така периметърът на триъгълник ABC е 24+20+16=60.

*Сега повече подробности за триъгълниците, получени чрез конструиране на трите средни линии. Тяхното равенство се доказва лесно. Виж:

Те са равни от три страни. Разбира се, тук важат и други признаци. Разбираме това

Как се използва това свойство в задачите, включени в изпита? Бих искал специално да обърна внимание на проблемите в стереометрията. Има видове, при които говорим за триъгълна призма.

Например, казва се, че равнината минава през средните точки на страните на основата и е успоредна на третия ръб на основата. Повдигат се въпроси относно промените в повърхността на призмата, нейния обем и др.

И така, ето го. Познавайки и разбирайки информацията, представена по-горе, вие веднага ще определите, че тази равнина отрязва една четвърт от основата на определената призма и ще решите проблема устно. С такива задачи.

Това е всичко! Всичко най-хубаво!

Изтеглете материал за статия

С уважение, Александър Крутицких.

Понякога темите, които се обясняват в училище, не винаги са ясни от първия път. Това важи особено за предмет като математиката. Но всичко става много по-сложно, когато тази наука започне да се разделя на две части: алгебра и геометрия.

Всеки ученик може да има способности в една от двете области, но особено в началните класове е важно да се разберат основите както на алгебрата, така и на геометрията. В геометрията една от основните теми се счита за раздела за триъгълниците.

Как да намерим средната линия на триъгълник? Нека да го разберем.

Основни понятия

Като начало, за да разберете как да намерите средната линия на триъгълник, е важно да разберете какво е това.

Няма ограничения за изчертаване на средната линия: триъгълникът може да бъде всякакъв (равнобедрен, равностранен, правоъгълен). И всички свойства, които се отнасят до средната линия, ще бъдат в сила.

Средната линия на триъгълник е отсечка, свързваща средните точки на двете му страни. Следователно всеки триъгълник може да има 3 такива линии.

Имоти

За да знаете как да намерите средната линия на триъгълник, нека обозначим неговите свойства, които трябва да се запомнят, в противен случай без тях ще бъде невъзможно да се решат проблеми с необходимостта да се посочи дължината на средната линия, тъй като всички получени данни трябва да бъдат обосновани и се аргументира с теореми, аксиоми или свойства.

По този начин, за да отговорите на въпроса: „Как да намерите средната линия на триъгълник ABC?“, Достатъчно е да знаете една от страните на триъгълника.

Да дадем пример

Разгледайте снимката. Показва триъгълник ABC със средна линия DE. Обърнете внимание, че тя е успоредна на основата AC в триъгълника. Следователно, каквато и да е стойността на AC, средната линия DE ще бъде наполовина по-голяма. Например AC=20 означава DE=10 и т.н.

По тези прости начини можете да разберете как да намерите средната линия на триъгълник. Запомнете неговите основни свойства и дефиниция и тогава никога няма да имате проблеми с намирането на значението му.

\[(\Large(\text(Сходство на триъгълници)))\]

Дефиниции

Два триъгълника се наричат ​​подобни, ако ъглите им са съответно равни и страните на единия триъгълник са пропорционални на еднаквите страни на другия
(страните се наричат ​​подобни, ако лежат срещу еднакви ъгли).

Коефициентът на подобие на (подобни) триъгълници е число, равно на съотношението на еднаквите страни на тези триъгълници.

Определение

Периметърът на триъгълник е сумата от дължините на всичките му страни.

Теорема

Отношението на периметрите на два подобни триъгълника е равно на коефициента на подобие.

Доказателство

Разгледайте триъгълници \(ABC\) и \(A_1B_1C_1\) със страни \(a,b,c\) и \(a_1, b_1, c_1\) съответно (вижте фигурата по-горе).

Тогава \(P_(ABC)=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_(A_1B_1C_1)\)

Теорема

Отношението на площите на два подобни триъгълника е равно на квадрата на коефициента на подобие.

Доказателство

Нека триъгълниците \(ABC\) и \(A_1B_1C_1\) са подобни и \(\dfrac(AB)(A_1B_1) = \dfrac(AC)(A_1C_1) = \dfrac(BC)(B_1C_1) = k\). Нека означим съответно с буквите \(S\) и \(S_1\) площите на тези триъгълници.

Тъй като \(\ъгъл A = \ъгъл A_1\) , тогава \(\dfrac(S)(S_1) = \dfrac(AB\cdot AC)(A_1B_1\cdot A_1C_1)\)(по теоремата за съотношението на площите на триъгълници с равни ъгли).

защото \(\dfrac(AB)(A_1B_1) = \dfrac(AC)(A_1C_1) = k\), Че \(\dfrac(S)(S_1) = \dfrac(AB)(A_1B_1)\cdot\dfrac(AC)(A_1C_1) = k\cdot k = k^2\), което трябваше да се докаже.

\[(\Large(\text(Признаци за подобие на триъгълници)))\]

Теорема (първият признак за подобие на триъгълници)

Ако два ъгъла на един триъгълник са съответно равни на два ъгъла на друг триъгълник, тогава тези триъгълници са подобни.

Доказателство

Нека \(ABC\) и \(A_1B_1C_1\) са триъгълници, така че \(\angle A = \angle A_1\) , \(\angle B = \angle B_1\) . След това, по теоремата за сумата от ъглите на триъгълник \(\ъгъл C = 180^\circ - \angle A - \angle B = 180^\circ - \angle A_1 - \angle B_1 = \angle C_1\), тоест ъглите на триъгълника \(ABC\) са съответно равни на ъглите на триъгълника \(A_1B_1C_1\) .

Тъй като \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\) , тогава \(\dfrac(S_(ABC))(S_(A_1B_1C_1)) = \dfrac(AB\cdot AC)(A_1B_1\cdot A_1C_1)\)И \(\dfrac(S_(ABC))(S_(A_1B_1C_1)) = \dfrac(AB\cdot BC)(A_1B_1\cdot B_1C_1)\).

От тези равенства следва, че \(\dfrac(AC)(A_1C_1) = \dfrac(BC)(B_1C_1)\).

По същия начин е доказано, че \(\dfrac(AC)(A_1C_1) = \dfrac(AB)(A_1B_1)\)(използвайки равенства \(\angle B = \angle B_1\) , \(\angle C = \angle C_1\) ).

В резултат на това страните на триъгълника \(ABC\) са пропорционални на подобните страни на триъгълника \(A_1B_1C_1\), което трябваше да се докаже.

Теорема (втори критерий за подобие на триъгълници)

Ако две страни на един триъгълник са пропорционални на две страни на друг триъгълник и ъглите между тези страни са равни, тогава триъгълниците са подобни.

Доказателство

Помислете за два триъгълника \(ABC\) и \(A"B"C"\), така че \(\dfrac(AB)(A"B")=\dfrac(AC)(A"C")\), \(\ъгъл BAC = \ъгъл A"\) Нека докажем, че триъгълниците \(ABC\) и \(A"B"C"\) са подобни. Като вземем предвид първия знак за подобие на триъгълници, достатъчно е да покажем, че \(\ъгъл B = \ъгъл B"\) .

Да разгледаме триъгълник \(ABC""\) с \(\ъгъл 1 = \ъгъл A"\) , \(\ъгъл 2 = \ъгъл B"\) . Триъгълниците \(ABC""\) и \(A"B"C"\) са подобни според първия критерий за сходство на триъгълниците, тогава \(\dfrac(AB)(A"B") = \dfrac(AC"")(A"C")\).

От друга страна, по условие \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C")\). От последните две равенства следва, че \(AC = AC""\) .

Триъгълниците \(ABC\) и \(ABC""\) са равни по две страни и ъгъл между тях, следователно, \(\ъгъл B = \ъгъл 2 = \ъгъл B"\).

Теорема (трети знак за подобие на триъгълници)

Ако три страни на един триъгълник са пропорционални на три страни на друг триъгълник, тогава триъгълниците са подобни.

Доказателство

Нека страните на триъгълниците \(ABC\) и \(A"B"C"\) са пропорционални: \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C") = \dfrac(BC)(B"C")\). Нека докажем, че триъгълниците \(ABC\) и \(A"B"C"\) са подобни.

За да направите това, като вземете предвид втория критерий за подобие на триъгълниците, е достатъчно да докажете, че \(\angle BAC = \angle A"\) .

Да разгледаме триъгълник \(ABC""\) с \(\ъгъл 1 = \ъгъл A"\) , \(\ъгъл 2 = \ъгъл B"\) .

Триъгълниците \(ABC""\) и \(A"B"C"\) са подобни според първия критерий за сходство на триъгълници, следователно, \(\dfrac(AB)(A"B") = \dfrac(BC"")(B"C") = \dfrac(C""A)(C"A")\).

От последната верига от равенства и условия \(\dfrac(AB)(A"B") = \dfrac(AC)(A"C") = \dfrac(BC)(B"C")\)следва, че \(BC = BC""\) , \(CA = C""A\) .

Триъгълниците \(ABC\) и \(ABC""\) са равни по три страни, следователно, \(\ъгъл BAC = \ъгъл 1 = \ъгъл A"\).

\[(\Large(\text(Теорема на Талес)))\]

Теорема

Ако маркирате равни сегменти от едната страна на ъгъл и начертаете успоредни прави линии през техните краища, тогава тези прави линии също ще отрежат равни сегменти от другата страна.

Доказателство

Нека първо докажем лема:Ако в \(\триъгълник OBB_1\) права линия \(a\паралел BB_1\) е начертана през средата \(A\) на страната \(OB\), тогава тя също ще пресича страната \(OB_1\) в средата.

През точката \(B_1\) начертаваме \(l\паралелен OB\) . Нека \(l\cap a=K\) . Тогава \(ABB_1K\) е успоредник, следователно \(B_1K=AB=OA\) и \(\ъгъл A_1KB_1=\ъгъл ABB_1=\ъгъл OAA_1\); \(\ъгъл AA_1O=\ъгъл KA_1B_1\)като вертикално. И така, според втория знак \(\триъгълник OAA_1=\триъгълник B_1KA_1 \Дясна стрелка OA_1=A_1B_1\). Лемата е доказана.

Да преминем към доказателството на теоремата. Нека \(OA=AB=BC\) , \(a\паралел b\паралел c\) и трябва да докажем, че \(OA_1=A_1B_1=B_1C_1\) .

Така, съгласно тази лема \(OA_1=A_1B_1\) . Нека докажем, че \(A_1B_1=B_1C_1\) . Нека начертаем права \(d\паралел OC\) през точката \(B_1\) и нека \(d\cap a=D_1, d\cap c=D_2\) . Тогава \(ABB_1D_1, BCD_2B_1\) са успоредници, следователно \(D_1B_1=AB=BC=B_1D_2\) . По този начин, \(\ъгъл A_1B_1D_1=\ъгъл C_1B_1D_2\)като вертикално \(\ъгъл A_1D_1B_1=\ъгъл C_1D_2B_1\)лежащи като кръстове и, следователно, според втория знак \(\триъгълник A_1B_1D_1=\триъгълник C_1B_1D_2 \Дясна стрелка A_1B_1=B_1C_1\).

Теорема на Талес

Успоредните линии отрязват пропорционални сегменти от страните на ъгъл.

Доказателство

Нека успоредни прави \(p\паралелен q\паралелен r\паралелен s\)раздели една от линиите на сегменти \(a, b, c, d\) . След това втората права линия трябва да бъде разделена съответно на сегменти \(ka, kb, kc, kd\), където \(k\) е определено число, същият коефициент на пропорционалност на сегментите.

Нека начертаем през точката \(A_1\) права \(p\паралелен OD\) (\(ABB_2A_1\) е успоредник, следователно \(AB=A_1B_2\) ). Тогава \(\триъгълник OAA_1 \sim \триъгълник A_1B_1B_2\)на два ъгъла. следователно \(\dfrac(OA)(A_1B_2)=\dfrac(OA_1)(A_1B_1) \Rightarrow A_1B_1=kb\).

По същия начин начертаваме права линия през \(B_1\) \(q\parallel OD \Rightarrow \triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\)и т.н.

\[(\Large(\text(Средна линия на триъгълника)))\]

Определение

Средната линия на триъгълник е отсечка, свързваща средните точки на произволни две страни на триъгълника.

Теорема

Средната линия на триъгълника е успоредна на третата страна и равна на половината от нея.

Доказателство

1) Успоредността на средната линия спрямо основата следва от доказаното по-горе леми.

2) Нека докажем, че \(MN=\dfrac12 AC\) .

През точката \(N\) начертаваме права, успоредна на \(AB\) . Нека тази права пресича страната \(AC\) в точката \(K\) . Тогава \(AMNK\) е успоредник ( \(AM\паралел NK, MN\паралел AK\)съгласно предходната точка). И така, \(MN=AK\) .

защото \(NK\паралел AB\) и \(N\) са средната точка на \(BC\), тогава според теоремата на Талес \(K\) е средната точка на \(AC\) . Следователно \(MN=AK=KC=\dfrac12 AC\) .

Последица

Средната линия на триъгълника отсича от него триъгълник, подобен на дадения с коефициент \(\frac12\) .

Нарича се четириъгълник, в който само две страни са успоредни трапец.

Успоредните страни на трапеца се наричат ​​негови причини, а онези страни, които не са успоредни, се наричат страни. Ако страните са равни, тогава такъв трапец е равнобедрен. Разстоянието между основите се нарича височина на трапеца.

Средна линия Трапец

Средната линия е сегмент, свързващ средните точки на страните на трапеца. Средната линия на трапеца е успоредна на основите му.

Теорема:

Ако правата, пресичаща средата на едната страна, е успоредна на основите на трапеца, тогава тя разполовява втората страна на трапеца.

Теорема:

Дължината на средната линия е равна на средноаритметичното от дължините на нейните основи

MN средна линия, AB и CD - основи, AD и BC - странични страни

MN = (AB + DC)/2

Теорема:

Дължината на средната линия на трапец е равна на средноаритметичното от дължините на основите му.

Основната задача: Докажете, че средната линия на трапец разполовява отсечка, чиито краища лежат в средата на основите на трапеца.

Средна линия на триъгълника

Отсечката, свързваща средите на двете страни на триъгълника, се нарича средна линия на триъгълника. Тя е успоредна на третата страна и дължината й е равна на половината от дължината на третата страна.
Теорема: Ако линия, пресичаща средата на едната страна на триъгълник, е успоредна на другата страна на триъгълника, тогава тя разполовява третата страна.

AM = MC и BN = NC =>

Прилагане на свойствата на средната линия на триъгълник и трапец

Разделяне на сегмент на определен брой равни части.
Задача: Разделете отсечката AB на 5 равни части.
Решение:
Нека p е произволен лъч с начало в точка A и който не лежи на правата AB. Последователно заделяме 5 равни сегмента на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 ​​​​A 5
Свързваме A 5 с B и начертаваме такива прави през A 4, A 3, A 2 и A 1, които са успоредни на A 5 B. Те пресичат AB съответно в точки B 4, B 3, B 2 и B 1. Тези точки разделят отсечката AB на 5 равни части. Наистина, от трапеца BB 3 A 3 A 5 виждаме, че BB 4 = B 4 B 3. По същия начин от трапеца B 4 B 2 A 2 A 4 получаваме B 4 B 3 = B 3 B 2

Докато от трапеца B 3 B 1 A 1 A 3, B 3 B 2 = B 2 B 1.
Тогава от B 2 AA 2 следва, че B 2 B 1 = B 1 A. В заключение получаваме:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно е, че за да разделим отсечката AB на друг брой равни части, трябва да проектираме същия брой равни отсечки върху лъча p. След това продължете по описания по-горе начин.